
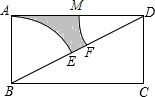
 如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π.
如图,已知矩形ABCD中,AB=8,BC=5π.分别以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,则图中阴影部分的面积为4π. 分析 由题意和图形可得,阴影部分的面积等于△ABD的面积与扇形ABE和扇形DMF的差,而两个扇形的半径相等,所对的圆心角的和等于90°,从而可以把两个扇形合在一起正好是四分之一个圆,然后计算出它们的面积作差,本题得以解决.
解答 解:∵在矩形ABCD中,AB=8,BC=5π,
∴∠BAC=90°,∠ABD+∠ADB=90°,BC=AD=5π,
∴${S}_{△ABD}=\frac{AB×AD}{2}=\frac{8×5π}{2}=20π$,
∵以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,以B,D为圆心,AB为半径画弧,两弧分别交对角线BD于点E,F,
∴S扇形ABE+S扇形DMF=$\frac{90°}{360°}×π×{8}^{2}=16π$,
∴S阴影AEMF=S△ABD-S扇形ABE-S扇形DMF=20π-16π=4π,
故答案为:4π.
点评 本题考查扇形面积的计算,解题的关键是明确题意,利用数形结合和转化的数学思想,来解答本题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:选择题
| A. | -2,1,0,1,2 | B. | -1,0,1,2,3 | C. | -2,-1,0,1 | D. | -1,0,1,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=1 | B. | (x+2)2=1 | C. | (x-2)2=7 | D. | (x+2)2=7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com