练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知a2+3b2+8a-18b+43=0，则a+3b=5．

    分析 利用配方法将已知等式转化为（a-4）2+3（b-3）2=0的形式，利用非负数的性质求得a、b的值，然后将其代入所求的代数式进行求值即可．

    解答 解：∵a2+3b2+8a-18b+43=（a+4）2+3（b-3）2=0
    ∴a+4=0，b-3=0，
    ∴a=-4，b=3．
    ∴a+3b=-4+3×3=5．
    故答案是：5．

    点评 本题考查了配方法的应用和非负数的性质．任意一个数的偶次方都是非负数，当几个数或式的偶次方相加和为0时，则其中的每一项都必须等于0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

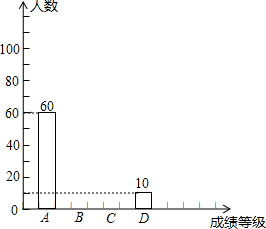    19．为了迎接党的十八大的召开，某校组织了以“党在我心中”为主题的征文比赛，每位学生只能参加一次比赛，比赛成绩分A、B、C、D四个等级．随机抽取该校部分学生的征文比赛成绩进行统计分析，并绘制了如下的统计图表：
    成绩等级ABCD
    人数60xy10
    占抽查学生总数的百分比30%50%15%m
    根据表中的信息，解决下列问题：
    （1）本次抽查的学生共有200名；
    （2）表中x、y和m所表示的数分别为：X=100，y=30，m=5%；补全条形统计图；
    （3）若获得A、B、C、D四个等级按分值分别记为每人5分、4分、3分、2分，现选取A等2人，B等2人，C等1人，D等1人组成6人小团队，利用树形图或列表法，求在这6人中随机抽取2人，2人分数之和不低于8分的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

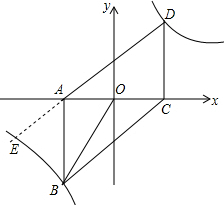    20．如图，在平面直角坐标系中，点 A、C关于原点O对称，分别过点A、C作x轴的垂线，它们与反比例函数y=$\frac{k}{x}$的图象交于点B、D，连结AD、BC，若C点的坐标为（m，0）
    （1）则A点的坐标是（-m，0）；
    （2）求证：四边形ABCD是平行四边形；
    （3）延长DA交反比例函数y=$\frac{k}{x}$的图象于另一点E（-10，-4），若m=5，在反比例函数y=$\frac{k}{x}$的图象上，是否存在点P，使得△ADP的面积等于△ABO的面积的2倍？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，内外两个四边形都是正方形，阴影部分的宽为4，且面积为56，则内部小正方的面积是？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如果x2-3x+1=0，求值：
    （1）x2+$\frac{1}{{x}^{2}}$；
    （2）x4+$\frac{1}{{x}^{4}}$；
    （3）$\frac{{x}^{2}}{{x}^{4}+3{x}^{3}+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：$\frac{{x}^{2}-6+9}{9-{x}^{2}}$÷$\frac{2x-6}{{x}^{2}+3x}$，其中x=（$\sqrt{2}$-1）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．分解因式求值：2012+20122-20132．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某工人加工300个零件，若每小时加工50个可按时完成，但他加工2小时后，因事停工40分钟，那么这个工人为了按时或提前完成任务，后面的时间每小时他至少要加工多少个零件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

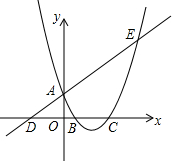    19．如图，已知直线y=$\frac{1}{2}$x+1与y轴交于点A，与x轴交于点D，抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．
    （1）求该抛物线的解析式；
    （2）动点P在x轴上移动，当△PAE是直角三角形时，求点P的坐标．

    查看答案和解析>>

    同步练习册答案