
【题目】已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为( )
A. 8 cm或10 cm B. 8 cm或9 cm C. 8 cm D. 10 cm
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)问题背景
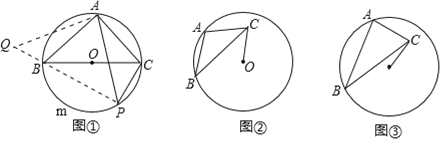
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证: ![]() PA=PB+PC.
PA=PB+PC.
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2 , 连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为![]() 米.
米.
(1)花圃的面积为 ![]() (用含
(用含![]() 的式子表示);
的式子表示);
(2)如果通道所占面积是整个长方形空地面积的![]() ,求出此时通道的宽;
,求出此时通道的宽;
(3)已知某园林公司修建通道、花圃的造价![]() (元)、
(元)、![]() (元)与修建面积
(元)与修建面积![]()
![]() 之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元
之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价为105920元

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com