
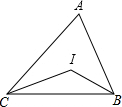
 如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:
如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:分析 由三角形内角和定理得∠ABC+∠ACB=180°-∠A,∠ABC与∠ACB的平分线交于点I,则∠IBC+∠ICB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A),在△IBC中,利用三角形内角和定理求∠BIC即可.①②代入求得答案即可.
解答 解:∠BIC=90°+$\frac{1}{2}$∠A
在△ABC中,∠ABC+∠ACB=180°-∠A
∵BI、CI是△ABC内角的平分线
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB
∴∠IBC+∠ICB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A)
在△IBC中,
∠BIC=180°-(∠IBC+∠ICB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A
即:∠BIC=90°+$\frac{1}{2}$∠A
①当∠A=50°时,∠BIC=115°.
②当∠BIC=130°时,∠A=80°.
点评 本题考查了三角形角平分线的性质,内角和定理的运用,掌握三角形的内角和等于180°是解决问题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
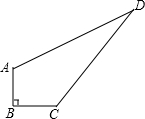 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
如图,点P是?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com