
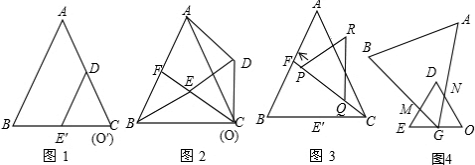
分析 (1)BE=AD,可通过证三角形BEC和ACD全等来得出.
(2)由于重合部分的面积无法直接求出,因此可用△RPQ的面积减去△RST的面积来求得(S、T为RP、RQ与AC的交点).△PRQ的面积易求得.关键是△RST的面积,三角形RST中,由于∠RTS=∠CTQ=60°-∠TCQ=30°,而∠R=60°,因此△RST是直角三角形,只需求出RS和ST的长即可.上面已经求得了∠QTC=∠QCT=30°,因此RT=RQ-QT=RQ-QC=3-x,然后根据△RTS中特殊角的度数即可得出RS和ST的长,进而可得出y,x的函数关系式.
(3)本题可通过证△GEM和△NGO相似来求解.
解答 解:(1)BE=AD.
证明:∵△ABC与△DCE是等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CE=CD,
∴∠BCE=∠ACD,
在△BCE与△ACD中,
$\left\{\begin{array}{l}{CA=CB}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)如图在△CQT中,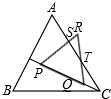
∵∠TCQ=30°∠RQP=60°,
∴∠QTC=30°,
∴∠QTC=∠TCQ,
∴QT=QC=x,
∴RT=2-x,
∵∠RTS+∠R=90°
∴∠RST=90°
∴y=$\frac{\sqrt{3}}{4}×{2}^{2}-\frac{\sqrt{3}}{8}(2-x)^{2}=-\frac{\sqrt{3}}{8}(2-x)^{2}+\sqrt{3}$(0≤x≤2).
(3)答:ON•EM的值不变,理由为:
证明:∵∠AGB=60°
∴∠MGE+∠NGO=120°
∵∠GNO+∠NGO=120°
∴∠MGE=∠GNO
∵∠E=∠O
∴△EMG∽△OGN
∴$\frac{EM}{OG}=\frac{EG}{ON}$,
∴ON•EM=OG•EG=1.
点评 此题考查了相似三角形的判定与性质,全等三角形的判定与性质以及一元二次方程的求解方法等知识.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
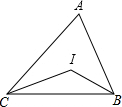 如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:
如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$是$\frac{4}{9}$的一个平方根 | B. | $\sqrt{2}$是$\sqrt{4}$的算术平方根 | ||
| C. | 平方根等于本身的数有0和1 | D. | (-4)2的算术平方根是4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
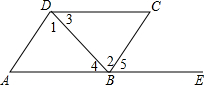 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠5 | D. | ∠A+∠ABC=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
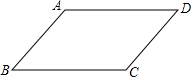 如图,下面推理中,正确的是( )
如图,下面推理中,正确的是( )| A. | ∵∠A+∠D=180°∴AD∥BC | B. | ∵∠C+∠D=180°∴AB∥CD | ||
| C. | ∵∠A+∠D=180°∴AB∥CD | D. | ∵∠B+∠C=180°∴AD∥BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
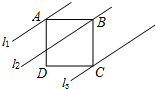 如图,已知正方形ABCD,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为3,l2与l3的距离为5,则正方形ABCD的面积等于( )
如图,已知正方形ABCD,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为3,l2与l3的距离为5,则正方形ABCD的面积等于( )| A. | 9 | B. | 25 | C. | 34 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com