练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
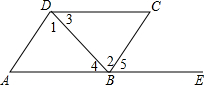
    16．如图，点A，B，E在一条直线上，下列条件中不能判断AD∥BC的是（　　）
    A．∠1=∠2B．∠3=∠4C．∠A=∠5D．∠A+∠ABC=180°

    分析 根据平行线的判定定理对各选项进行逐一判断即可．

    解答 解：A、∵∠1=∠2，∴AD∥BC，故本选项错误；
    B、∵∠3=∠4，∴AB∥CD，故本选项正确；
    C、∵∠1=∠2，∴AD∥BC，故本选项错误；
    D、∵∠A+∠ABC=180°，∴AD∥BC，故本选项错误．
    故选B．

    点评 本题考查的是平行线的判定定理，用到的知识点为：同旁内角互补，两直线平行；同位角相等，两直线平行；内错角相等，两直线平行是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

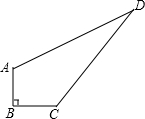    6．老张家有一块草坪如图所示．家里想整理它，需要知道其面积．老张测量了草坪各边得知：AB=3米，BC=4米，AD=12米，CD=13米，且AB⊥CB．请你帮老张家计算一下这块草坪的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，点P是?ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
    ①S1+S3=S2+S4     
    ②如果S4＞S2，则S3＞S1
    ③若S3=2S1，则S4=2S2
    ④若S1-S2=S3-S4，则P点一定在对角线BD上．
    其中正确结论的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．图1是边长分别为4$\sqrt{3}$和2的两个等边三角形纸片ABC和ODE叠放在一起（C与O重合）．
    （1）操作：固定△ABC，将△0DE绕点C顺时针旋转30°后得到△ODE，连结AD、BE，CE的延长线交AB于F（图2）；
    探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
    （2）在（1）的条件下将的△ODE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR，当点P与点F重合时停止运动（图3）
    探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
    （3）将图1中△0DE固定，把△ABC沿着OE方向平移，使顶点C落在OE的中点G处，设为△ABG，然后将△ABG绕点G顺时针旋转，边BG交边DE于点M，边AG交边DO于点N，设∠BGE=α（30°＜α＜90°）；（图4）
    探究：在图4中，线段ON•EM的值是否随α的变化而变化？如果没有变化，请你求出ON•EM的值，如果有变化，请你说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为4和10，则b的面积为14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：${（{-2}）^2}+|{\sqrt{2}-\sqrt{3}}|-\sqrt{3}+\root{3}{-64}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，已知，AB∥CD，B是∠AOC的角平分线OE的反向延长线与直线AB的交点，若∠A+∠C=90°，∠ABE=15°，则∠C=60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图1，正方形ABCD中，E，F分别是边BC，CD上的点，AF与ED相交于O，且BE=CF，过点C作CG⊥DE，垂足为G．
    （1）求证：DE⊥AF；
    （2）探究：线段AO，DO，GO长度之间存在怎样的数量关系？请写出并说明理由；
    （3）拓展：若点E，F分别在线段BC，CD的延长线上，AF与ED的延长线相交于O，其余条件不变，请你在图2中画出满足条件的图形，并写出线段AO，DO，GO长度之间的数量关系（不需证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．顺次连接对角线互相垂直的四边形的中点的四边形是（　　）
    A．矩形B．直角梯形C．菱形D．正方形

    查看答案和解析>>

    同步练习册答案