
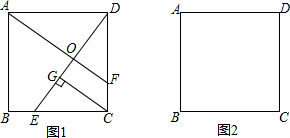
���� ��1����BE=CF�������ε����ʣ��ó�CE=DF��DC=AD����DCE=��ADF=90�㣬֤����CDE�ա�DAF���ó���CDE=��DAF������CDE+��ADO=90�㣬�ɵá�DAF+��ADO=90�㣬���û����ϵ�ó���AOD=90�㼴�ɣ�
��2���ɣ�1���Ľ��ۿ�֤��ADO�ա�DCG����AO=DG=DO+OG��
��3���������⻭��ͼ�Σ�ͬ��1���á�ADF�ա�DCE��֤�á�AOD=90�㣬֤�á�ADO�ա�DCG����ȫ�������ε����ʿɵ�AO=DG��OD=CG�������������ν�Ͽɵý��ۣ�
��� ��1��֤�������ı���ABCDΪ�����Σ���BE=CF��
��CE=DF��DC=AD����DCE=��ADF=90�㣬
�ڡ�CDE�͡�DAF�У�
$\left\{\begin{array}{l}{CE=DF}\\{��ECD=��FDA=90��}\\{CD=DA}\end{array}\right.$��
���CDE�ա�DAF��
���CDE=��DAF��
�֡ߡ�CDE+��ADO=90�㣬
���DAF+��ADO=90�㣬
���AOD=90�㣬��DE��AF��
��2���⣺AO=DO+OG��
���ɣ��ɣ�1���Ľ��ۿ�֪��
��CDE=��DAF����AOD=��DGC=90�㣬AD=DC��
�ڡ�ADO�͡�DCG�У�
$\left\{\begin{array}{l}{��AOD=��DGC=90��}\\{��DAF=��CDE}\\{AD=DC}\end{array}\right.$��
���ADO�ա�DCG��
����AO=DG=DO+OG��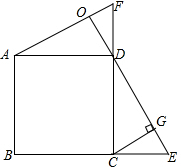
��3���⣺��ͼ��Ϊ����
��ͼ��ʾ��AO+DO=GO��
���ɣ���ͬ��1���ɵá�ADF�ա�DCE��
���DAF=��CDE��
�ߡ�CDE=��FDO��
���DAF=��FDO��
�ߡ�FDO+��ADO=90�㣬
���DAF+��ADO=90�㣬
���AOD=90�㣬
�ڡ�ADO���DCG�У�
$\left\{\begin{array}{l}{��AOD=��DGC=90��}\\{��DAO=��CDG}\\{AD=DC}\end{array}\right.$��
���ADO�ա�DCG��
��AO=DG��OD=CG��
��OD+DG=OG��
��OD+AO=GO��
���� ������Ҫ������ȫ�������ε��ж������ʣ������ε����ʣ��ؼ������������ε�����֤��ȫ�������Σ������߶Σ��ǵĹ�ϵ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
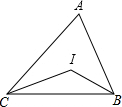 ��ͼ���ڡ�ABC����ABC�͡�ACB�Ľ�ƽ�����ཻ��I���ʡ�BIC���A��ʲô��ϵ������������ϵ�����㣺
��ͼ���ڡ�ABC����ABC�͡�ACB�Ľ�ƽ�����ཻ��I���ʡ�BIC���A��ʲô��ϵ������������ϵ�����㣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
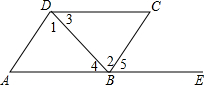 ��ͼ����A��B��E��һ��ֱ���ϣ����������в����ж�AD��BC���ǣ�������
��ͼ����A��B��E��һ��ֱ���ϣ����������в����ж�AD��BC���ǣ�������| A�� | ��1=��2 | B�� | ��3=��4 | C�� | ��A=��5 | D�� | ��A+��ABC=180�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
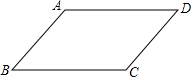 ��ͼ�����������У���ȷ���ǣ�������
��ͼ�����������У���ȷ���ǣ�������| A�� | �ߡ�A+��D=180���AD��BC | B�� | �ߡ�C+��D=180���AB��CD | ||
| C�� | �ߡ�A+��D=180���AB��CD | D�� | �ߡ�B+��C=180���AD��BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
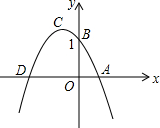 ��ͼ�Ƕ��κ���y=mx2+nx+b��ͼ����֪���Ķ���C�ڵڶ����ޣ��Ҿ�����A��1��0������B��0��1������x����һ����ΪD������ACD�����Ϊ��ABD�����$\frac{3}{2}$��ʱ��m��ֵΪ��������
��ͼ�Ƕ��κ���y=mx2+nx+b��ͼ����֪���Ķ���C�ڵڶ����ޣ��Ҿ�����A��1��0������B��0��1������x����һ����ΪD������ACD�����Ϊ��ABD�����$\frac{3}{2}$��ʱ��m��ֵΪ��������| A�� | $\sqrt{3}$-2 | B�� | -2��$\sqrt{3}$ | C�� | 2-$\sqrt{3}$ | D�� | -2-$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
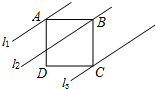 ��ͼ����֪������ABCD��ֱ��l1��l2��l3�ֱ�ͨ��A��B��C���㣬��l1��l2��l3����l1��l2�ľ���Ϊ3��l2��l3�ľ���Ϊ5����������ABCD��������ڣ�������
��ͼ����֪������ABCD��ֱ��l1��l2��l3�ֱ�ͨ��A��B��C���㣬��l1��l2��l3����l1��l2�ľ���Ϊ3��l2��l3�ľ���Ϊ5����������ABCD��������ڣ�������| A�� | 9 | B�� | 25 | C�� | 34 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com