
科目:初中数学 来源: 题型:选择题
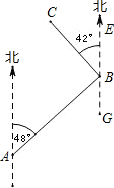 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )
如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东48°,A、B两地同时开工,若干天后公路准确接通.若公路AB长10千米另一条公路BC长7千米,且BC的走向是北偏西42°,则A到公路BC的距离为( )| A. | 3 | B. | 7 | C. | 10 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
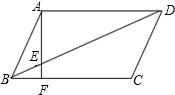 如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
如图,在?ABCD中,∠ABC=72°,AF⊥BC于F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )| A. | 60° | B. | 66° | C. | 70° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
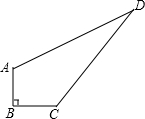 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com