【题目】如图，
的三边
的长分别为
，其三条角平分线交于点
，则
=______．
【答案】
【解析】
首先过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，由OA，OB，OC是△ABC的三条角平分线，根据角平分线的性质，可得OD=OE=OF，又由△ABC的三边AB、BC、CA长分别为40、50、60，即可求得S△ABO：S△BCO：S△CAO的值．
解：过点O作OD⊥AB于点D，作OE⊥AC于点E，作OF⊥BC于点F，
∵OA，OB，OC是△ABC的三条角平分线，
∴OD=OE=OF，
∵△ABC的三边AB、BC、CA长分别为40、50、60，
∴S△ABO：S△BCO：S△CAO=（
ABOD）：（BCOF）：（ACOE）
=AB：BC：AC=40：50：60=．
故答案为：．
黄冈创优卷系列答案科目：初中数学 来源： 题型：
【题目】四边形
是正方形，
是直线
上任意一点，
于点
，
于点
.当点G在BC边上时（如图1），易证DF-BE=EF.
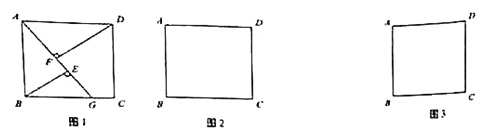
（1）当点在延长线上时，在图2中补全图形，写出
、
、
的数量关系，并证明；
（2）当点在
延长线上时，在图3中补全图形，写出、、的数量关系，不用证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
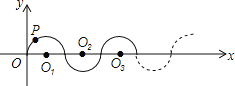
【题目】如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒
个单位长度，则第2019秒时，点P的坐标是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
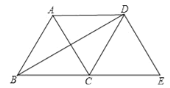
【题目】如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是________________(填写正确的序号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:如图，正方形ABCD，E为边AD上一点，△ABE绕点A逆时针旋转90°后得到△ADF．
⑴ 如果∠AEB＝65°，求∠DFE的度数；
⑵ BE与DF的数量关系如何?说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
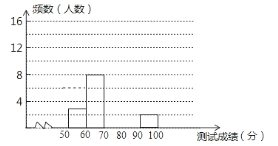
【题目】为了增强学生环保意识，我区举办了首届“环保知识大赛”，经选拔后有30名学生参加决赛，这30，名学生同事解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 50≤x＜60 | 3 |
第2组 | 60≤x＜70 | 8 |
第3组 | 70≤x＜80 | 13 |
第4组 | 80≤x＜90 | a |
第5组 | 90≤x＜100 | 2 |
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（4）第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导，则第4组的小宇与小强能同时抽到的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面内，菱形 ABCD 的对角线相交于点 O，点 O 又是菱形B1A1OC1的一个顶点，菱形 ABCD≌菱形 B1A1OC1，AB=BD=10．菱形B1A1OC1 绕点 O 转动，求两个菱形重叠部分面积的取值范围，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次，每次射耙的成绩情况如图所示：
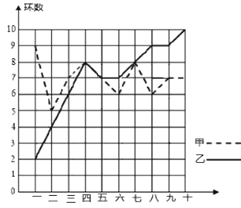
（1）请将下表补充完整：
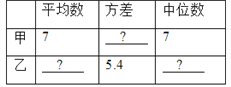
（2）请从下列三个不同的角度对这次测试结果进行分析：
①从平均数和方差相结合看， 的成绩好些；
②从平均数和中位数相结合看， 的成绩好些；
③若其他队选手最好成绩在9环左右，现要选一人参赛，你认为选谁参加，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AD∥BC，点E为CD上一点，AE，BE分别平分∠DAB，∠CBA．
（1）求证：AE⊥BE；
（2）求证：DE=CE；
（3）若AE=4，BE=6，求四边形ABCD的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com