
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况探索结论
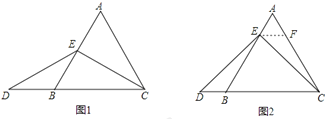
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE__________DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
【答案】(1)=;(2)=,证明见解析;(3)3或1.
【解析】
试题分析:本题主要考查全等三角形的判定和性质及等边三角形的性质和判定,利用全等得到BD=EF,再找EF和AE的关系是解题的关键.
(1)当E为中点时,过E作EF∥BC交AC于点F,则可证明△BDE≌△FEC,可得到AE=DB;
(2)类似(1)过E作EF∥BC交AC于点F,可利用AAS证明△BDE≌△FEC,可得BD=EF,再证明△AEF是等边三角形,可得到AE=EF,可得AE=DB;
(3)分点E在AB上和在BA的延长线上,类似(2)证得全等,再利用平行得到.
试题解析:
(1)答案为:=.
(2)答案为:=.
在等边△ABC中,∠ABC=∠ACB=∠BAC=60°,AB=BC=AC,
∵EF∥BC,
∴∠AEF=∠ABC,∠AFE=∠ACB,
∴∠AEF=∠AFE=∠BAC=60°,
∴AE=AF=EF,
∴AB﹣AE=AC﹣AF,
即BE=CF,
∵∠ABC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∵ED=EC,
∴∠EDB=∠ECB,
∵∠EBC=∠EDB+∠BED,∠ACB=∠ECB+∠FCE,
∴∠BED=∠FCE,
在△DBE和△EFC中,
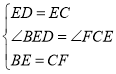 ,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
∴AE=BD.
(3)解:分为四种情况:
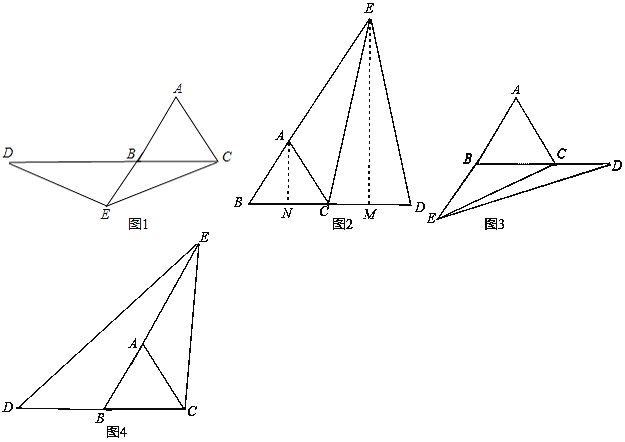
如图1:
∵AB=AC=1,AE=2,
∴B是AE的中点,
∵△ABC是等边三角形,
∴AB=AC=BC=1,△ACE是直角三角形(根据直角三角形斜边的中线等于斜边的一半),
∴∠ACE=90°,∠AEC=30°,
∴∠D=∠ECB=∠BEC=30°,∠DBE=∠ABC=60°,
∴∠DEB=180°﹣30°﹣60°=90°,
即△DEB是直角三角形.
∴BD=2BE=2(30°所对的直角边等于斜边的一半),
即CD=1+2=3.
如图2,
过A作AN⊥BC于N,过E作EM⊥CD于M,
∵等边三角形ABC,EC=ED,
∴BN=CN=![]() BC=
BC=![]() ,CM=MD=
,CM=MD=![]() CD,AN∥EM,
CD,AN∥EM,
∴△BAN∽△BEM,
∴![]() =
=![]() ,
,
∵△ABC边长是1,AE=2,
∴![]() =
=![]() ,
,
∴MN=1,
∴CM=MN﹣CN=1﹣![]() =
=![]() ,
,
∴CD=2CM=1;
如图3,∵∠ECD>∠EBC(∠EBC=120°),而∠ECD不能大于120°,否则△EDC不符合三角形内角和定理,
∴此时不存在EC=ED;
如图4,
∵∠EDC<∠ABC,∠ECB>∠ACB,
又∵∠ABC=∠ACB=60°,
∴∠ECD>∠EDC,
即此时ED≠EC,
∴此时情况不存在,
答:CD的长是3或1.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年参观“5.18”海交会的总人数约为489000人,将489000用科学记数法表示为( )
A.48.9×104
B.4.89×105
C.4.89×104
D.0.489×106
查看答案和解析>>
科目:初中数学 来源: 题型:
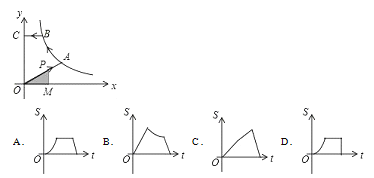
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
查看答案和解析>>
科目:初中数学 来源: 题型:
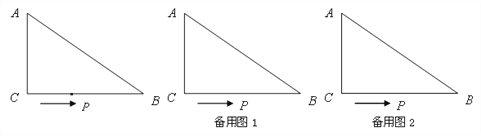
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
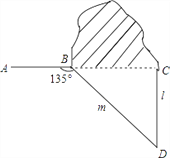
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com