
【题目】如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.
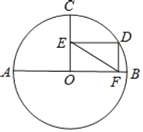
(1)求EF的长.
(2)若点E为OC的中点,
①求弧CD的度数.
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
【答案】(1)EF=6;(2)①弧CD的度数为60°;②PC+PD的最小值为6![]() .
.
【解析】
(1)求出圆的半径,再判断出四边形OFDE是矩形,再根据对角线相等即可解答;
(2)①根据线段中点的定义得到OE=![]() OC=
OC=![]() OD,根据三角形内角和得到∠DOE=60°,继而得到结论;②延长CO交⊙O于G,连接DG交AB于P,则PC+PD的最小值=DG,解直角三角形即可得到结论.
OD,根据三角形内角和得到∠DOE=60°,继而得到结论;②延长CO交⊙O于G,连接DG交AB于P,则PC+PD的最小值=DG,解直角三角形即可得到结论.
解:(1)连接OD,
∵⊙O的直径AB=12,
∴圆的半径为12÷2=6,
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=6;
(2)①∵点E为OC的中点,
∴OE=![]() OC=
OC=![]() OD,
OD,
∴∠EDO=30°,
∴∠DOE=60°,
∴弧CD的度数为60°;
②延长CO交⊙O于G,连接DG交AB于P,
则PC+PD的最小值=DG,
∵∠G=![]() ∠COD=30°,
∠COD=30°,
∵EG=9,
∴DG=![]() =
=![]() =
=![]() ,
,
∴PC+PD的最小值为![]() .
.


科目:初中数学 来源: 题型:
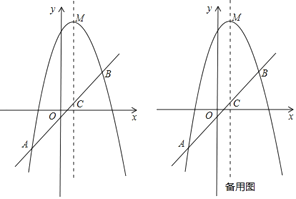
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
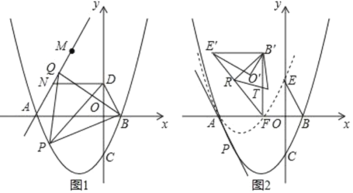
【题目】如图,在平面直角标系中,抛物线C:y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为y轴正半轴上一点.且满足OD=![]() OC,连接BD,
OC,连接BD,
(1)如图1,点P为抛物线上位于x轴下方一点,连接PB,PD,当S△PBD最大时,连接AP,以PB为边向上作正△BPQ,连接AQ,点M与点N为直线AQ上的两点,MN=2且点N位于M点下方,连接DN,求DN+MN+![]() AM的最小值
AM的最小值
(2)如图2,在第(1)问的条件下,点C关于x轴的对称点为E,将△BOE绕着点A逆时针旋转60°得到△B′O′E′,将抛物线y=![]() 沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
沿着射线PA方向平移,使得平移后的抛物线C′经过点E,此时抛物线C′与x轴的右交点记为点F,连接E′F,B′F,R为线段E’F上的一点,连接B′R,将△B′E′R沿着B′R翻折后与△B′E′F重合部分记为△B′RT,在平面内找一个点S,使得以B′、R、T、S为顶点的四边形为矩形,求点S的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
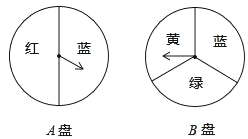
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园的工人需要摘苹果园和梨园的果实,苹果园的果实是梨园的![]() 倍,如果前三天工人都在苹果园摘果实,第四天,
倍,如果前三天工人都在苹果园摘果实,第四天,![]() 的工人到梨园摘果实,剩下
的工人到梨园摘果实,剩下![]() 的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是
的工人仍在苹果园摘果实,则第四天结束后苹果园的果实全部摘完,梨园剩下的果实正好是![]() 名工人
名工人![]() 天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
天的工作量.如果前三天工人都在苹果园摘果实,要使苹果和梨同时摘完,则第四天开始,再外请一个工人的情况下,应该安排___人摘苹果.(假定工人们每人每天摘果实的数量是相等的,且每人每天的工作时间相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
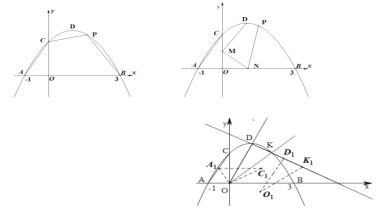
【题目】如图,抛物线![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 点的右侧),与
点的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线的顶点,且
为抛物线的顶点,且![]() .
.
(1)点![]() 为直线
为直线![]() 上方抛物线上一点,求四边形
上方抛物线上一点,求四边形![]() 的面积的最大值;点
的面积的最大值;点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 上的动点,当四边形
上的动点,当四边形![]() 面积取得最大值时,求当线段
面积取得最大值时,求当线段![]() 的值为最小值时点
的值为最小值时点![]() 的坐标.
的坐标.
(2)把![]() 绕点
绕点![]() 旋转一定角度后得到
旋转一定角度后得到![]() ,且点
,且点![]() 恰好在线段
恰好在线段![]() 上,抛物线上的点
上,抛物线上的点![]() 与点
与点![]() 关于抛物线对称轴对称,作
关于抛物线对称轴对称,作![]() ,把
,把![]() 沿直线
沿直线![]() 平移后得到
平移后得到![]() ,在变换过程中是否存在
,在变换过程中是否存在![]() 为等腰三角形,若存在,直接写出此时
为等腰三角形,若存在,直接写出此时![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a﹣1)x2+2x+a﹣1=0.
(1)若该方程有一根为2,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个根?求出此时a的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅(购买的数量不超过8吨),包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(单位:吨)之间的函数关系如图所示.
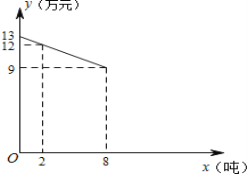
(1)求y与x的函数表达式?
(2)当销售数量为多少时,该公司经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)
(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是![]()
①当该公司销售杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样?
②该公司销售杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com