练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．1÷$\frac{3a}{2b}•\frac{9a}{4b}•\frac{3b}{2a}$=$\frac{9b}{4a}$．

    分析 原式利用除法法则变形，约分即可得到结果．

    解答 解：原式=1•$\frac{2b}{3a}$•$\frac{9a}{4b}$•$\frac{3b}{2a}$=$\frac{9b}{4a}$，
    故答案为：$\frac{9b}{4a}$

    点评 此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．已知圆柱的体积公式V=S•h．
    （1）若圆柱体积V一定，圆柱的高h（cm）与底面积S（cm2）之间是h=$\frac{V}{S}$函数关系：
    （2）若圆柱体体积一定，且S=3cm2时，h=16cm．求：
    ①h（cm）与S（cm2）之间的函数关系式：
    ②S=4cm2时h的值以及h=4cm时S的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．用因式分解计算：
    （1）10012-202202+1012；
    （2）20152+20162-4030×2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知平方差公式（a+b）（a-b）=a2-b2，则a2-b2=（a+b）（a-b），请利用后面的式子来计算1002-992+982-972+…+22-1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．一个三位数，百位数字是a，十位数字是b，个位数字是c，把百位数字a与个位数字c交换位置后，所得的新数与原数作差．试说明这个差能被99整除．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在?ABCD中，AB=3，AD=$\sqrt{2}$，∠B=135°，求?ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

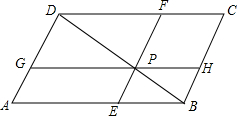    13．如图，在?ABCD中，P是对角线BD上的任意一点，过点P作EF∥BC，分别与AB，CD相交于点E，F；过点P再作GH∥AB，分别与AD，BC相交于点G，H，图中有几个平行四边形？其中哪几对平行四边形面积相等？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．下表是两种类型的电话计费方式．
    类型收费方式
    都市通月租费25元，被叫免费，主叫：3分钟以内，收费0.2元；超过3分钟的部分．每分钟0.1元，不足1分钟按1分钟计
    环球通月租费10元，主叫、被叫都按每分钟0.1元计费，不足1分钟按1分钟计
    （1）某都市通用户某次主叫时间为3分钟25秒，求这次通话产生的费用；
    （2）请根据下表（由环球通用户某月的电话清单整理），计算该用户这个月的费用：
    主叫被叫
    通话时间长/分钟234345
    次数10251525205
    （3）若某用户每月主叫与被叫的次数一样多，每次主叫与被叫的时间在1分钟以内，1到2分钟以内，2到3分钟以内，3到4分钟以内的次数之比为4：3：1：1．请根据他的通话次数确定选择什么类型的电话计费方式，才能使每月的费用最省？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

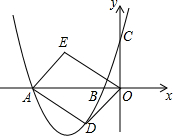    8．如图，在平面直角坐标系中，抛物线y=ax2+bx+3与x轴交于点A（-4，0），B（-1，0）两点．
    （1）求抛物线的解析式；
    （2）在第三象限的抛物线上有一动点D．如图，若四边形ODAE是以OA为对角线的平行四边形，当平行四边形ODAE的面积为6时，请判断平行四边形ODAE是否为菱形？说明理由．

    查看答案和解析>>

    同步练习册答案