
 如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.
如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4. 分析 先根据一次函数的解析式,得到一次函数y=kx-4k+5的图象经过点(4,5),过点(4,5)分别作y轴与x轴的垂线,分别交反比例函数图象于B点和C点,根据点A(p,q)只能在B点与C点之间,即可求得p的取值范围是$\frac{3}{5}$<p<4.
解答  解:一次函数y=kx-4k+5中,令x=4,则y=5,
解:一次函数y=kx-4k+5中,令x=4,则y=5,
故一次函数y=kx-4k+5的图象经过点(4,5),
如图所示,过点(4,5)分别作y轴与x轴的垂线,分别交反比例函数图象于B点和C点,
把y=5代入y=$\frac{3}{x}$,得x=$\frac{3}{5}$;
把x=4代入y=$\frac{3}{x}$,得y=$\frac{3}{4}$,
所以B点坐标为($\frac{3}{5}$,5),C点坐标为(4,$\frac{3}{4}$),
因为一次函数y的值随x的值增大而增大,
所以点A(p,q)只能在B点与C点之间的曲线上,
所以p的取值范围是$\frac{3}{5}$<p<4.
故答案为:$\frac{3}{5}$<p<4.
点评 本题考查了反比例函数图象与一次函数的交点问题:反比例函数与一次函数的图象的交点坐标满足两函数的解析式.解决问题的关键是确定点A在曲线上的位置.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
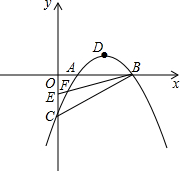 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 6 | 0.15 |
| B | 80≤x<90 | 20 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | 0.15 |
| 合计 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com