
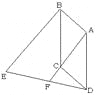
【题目】已知:如图,∠B=∠C,BD=CE,AB=DC,
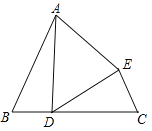
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
【答案】①见解析;②见解析.
【解析】
①先根据∠B=∠C,BD=CE,AB=DC,判定△ABD≌DCE,得出DA=DE,进而得到△ADE为等腰三角形;
②根据△ABD≌△DCE,得出∠BAD=∠CDE,再根据三角形内角和定理和平角的定义,得到∠ADE=60°,最后可判定等腰△ADE为等边三角形.
①在△ABD和△DCE中,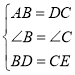 ,
,
∴△ABD≌△DCE(SAS),
∴DA=DE,
即△ADE为等腰三角形
②∵△ABD≌△DCE,
∴∠BAD=∠CDE,
∵∠B=60°,
∴∠BAD+∠ADB=120°,
∴∠CDE+∠ADB=120°,
∴∠ADE=60°,
又∵△ADE为等腰三角形,
∴△ADE为等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(重温旧知)圆内接四边形的内角具有特殊的性质.
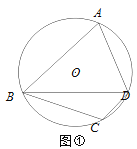
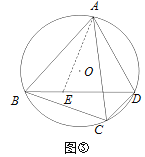
如图①,四边形ABCD是⊙O的内接四边形,若AB=BD,∠ABD=50°,则∠BCD=_______°.
(提出问题)圆内接四边形的边会有特殊性质吗?
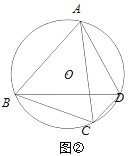
如图②,某数学兴趣小组进行深入研究发现:ABCD+BCDA=ACBD,请按他们的思路继续完成证明.
证明:如图③,作∠BAE=∠CAD,交BD于点E.
∵∠BAE=∠CAD,∠ABD=∠ACD,
∴△ABE∽△ACD,
∴![]() 即ABCD=ACBE
即ABCD=ACBE
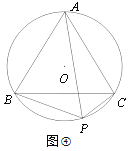
(应用迁移)如图,已知等边△ABC外接圆⊙O,点P为![]() 上一点,且PB=
上一点,且PB=![]() ,PC=1,求PA的长.
,PC=1,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四个2可以组成这样的数:
①2222,②2222,③![]() ,④
,④![]() ,⑤2222,⑥2222
,⑤2222,⑥2222
(1)其中最大的数是 ,(写序号)最小的数是 (写序号);
(2)用四个1组成一个数,最大的数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些数排列成下表中的四列:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
(1)第4行第1列的数是多少?直接写出答案;
(2)第17行的四个数之和是多少?请写出适当的过程;
(3)数100所在的行和列分别是多少?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场春节促销活动出售![]() 两种商品,活动方案如下两种:
两种商品,活动方案如下两种:
方案一 |
|
| |
每件标价 | 90元 | 100元 | |
每件商品返利 | 按标价的 | 按标价的 | |
例如买一件 | |||
方案二 | 所购商品一律按标价20%的返利 | ||
(1)某单位购买![]() 商品
商品![]() 件,
件,![]() 商品20件,选用何种方案划算?
商品20件,选用何种方案划算?
(2)某单位购买![]() 商品件(
商品件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少?
商品的件数是商品件数的2倍多1件。则两种方案的实际付款各多少?
(3)若两种方案的实际付款一样,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
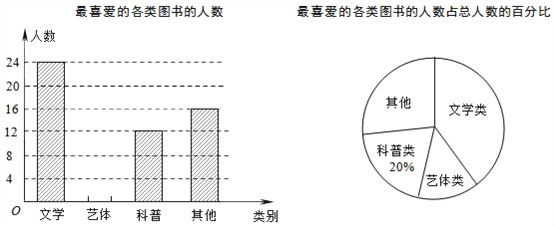
【题目】某出版社为了了解在校大学生最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),在广州某大学进行随机调查,并将调查结果绘制成如下两幅不完整的统计图(如图所示),请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有12000名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:把对角线互相垂直的四边形叫做“对角线垂直四边形”.
如图,在四边形![]() 中,
中,![]() ,四边形
,四边形![]() 就是“对角线垂直四边形”.
就是“对角线垂直四边形”.
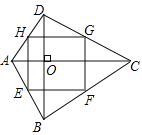
(1)下列四边形,一定是“对角线垂直四边形”的是_________.
①平行四边形 ②矩形 ③菱形 ④正方形
(2)如图,在“对角线垂直四边形”![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:EF=DF;
(2)若AC=2CF,∠ADC=60 o, AC⊥DC,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”.如图1在![]() 中,若
中,若![]() ,则
,则![]() 是“和谐三角形”.
是“和谐三角形”.

(1)等边三角形一定是“和谐三角形”,是______命题(填“真”或“假”).
(2)若![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 是“和谐三角形”,求
是“和谐三角形”,求![]() .
.
(3)如图2,在等边三角形![]() 的边
的边![]() ,
,![]() 上各取一点
上各取一点![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的高,若
的高,若![]() 是“和谐三角形”,且
是“和谐三角形”,且![]() .
.

①求证:![]() .
.
②连结![]() ,若
,若![]() ,那么线段
,那么线段![]() ,
,![]() ,
,![]() 能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
能否组成一个“和谐三角形”?若能,请给出证明:若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com