
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
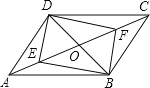
A.∠ADE=∠CBFB.∠ABE=∠CDFC.DE=BFD.OE=OF
【答案】C
【解析】
根据平行四边形的性质,以及平行四边形的判定定理即可作出判断.
A、在平行四边形ABCD中,
∵AO=CO,DO=BO,AD∥BC,AD=BC,
∴∠DAE=∠BCF,
若∠ADE=∠CBF,
在△ADE与△CBF中,
 ,
,
∴△ADE≌△CBF,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
B、若∠ABE=∠CDF,
在△ABE与△CDF中,
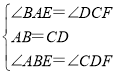 ,
,
∴△ABE≌△CDF,
∴AE=CF,
∵AO=CO,
∴OE=OF,
∵OD=OB,
∴四边形DEBF是平行四边形;
C、若DE与AC不垂直,则满足AC上一定有一点M使DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
D、若OE=OF,
∵OD=OB,
∴四边形DEBF是平行四边形;
故选C.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
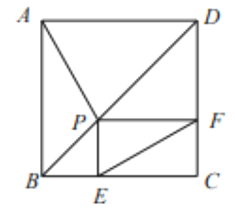
【题目】如图,己知正方形ABCD的边长为4, P是对角线BD上一点,PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=![]() EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF;⑤EF的最小值为![]() ;⑥AP⊥EF.其中正确结论的序号为( )
;⑥AP⊥EF.其中正确结论的序号为( )
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
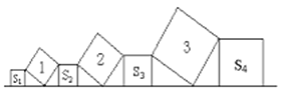
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有着丰富的土地资源,适宜种植玉米,某企业已收购玉米52.5吨,根据市场信息,将玉米直接销售,每吨可获利100元;如果对玉米进行粗加工,每天可加工8吨,每吨可获利1000元;如果对玉米进行精加工,每天可加工0.5吨,每吨可获利5000元.由于受条件限制,在同一天中只能采取一种加工方式,并且必须在30天内将这批玉米全部销售,为此,研究了两种方案.
(1)方案一:将玉米全部粗加工后销售,则可获利 元;
(2)方案二:30天时间都进行精加工,未来得及加工的玉米,在市场上直接销售,则可获利 元;
(3)问是否存在第三种方案,将部分玉米精加工,其余玉米粗加工,并恰好在30天内完成?若存在,请求销售后所获利润:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
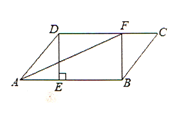
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
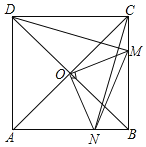
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),CN⊥DM,CN与AB交于点N,连接OM、ON、MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③AN2+CM2=MN2;④若AB=2,则S△OMN的最小值是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
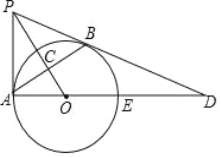
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com