
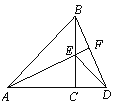
【题目】如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F。
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论。
【答案】(1)、证明过程见解析;(2)、证明过程见解析.
【解析】
试题分析:(1)、根据等腰直角三角形的性质得出AC=BC,EC=CD,∠BCD=∠ACB=90°,从而得到三角形全等;(2)、直线AE与BD互相垂直就是证明∠AFD=90°,根据三角形全等得到∠AEC=∠BDC,结合∠BEF=∠AEC,从而得出∠BEF=∠BDC,根据DBC+∠BDC=90°得到∠BEF+∠DBC=90°,从而得到垂直.
试题解析:(1)、∵△ACB和△ECD都是等腰直角三角形,∴AC=BC EC=CD,
又∵∠BCD=∠ACB=90°,∴△ACE≌△BCD(SAS)
(2)、∵△ACE≌△BCD ∴∠AEC=∠BDC,又∵∠BEF=∠AEC(对顶角),
∴∠BEF=∠BDC,又∵∠DBC+∠BDC=90°,∴∠BEF+∠DBC=90°,∴AF⊥BD,所以直线AE与BD互相垂直。


科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
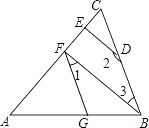
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是 ( )
A. 任意两个矩形形状相同 B. 任意两个菱形形状相同
C. 任意两个直角三角形相似 D. 任意两个正五边形形状相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com