
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上. 
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
【答案】
(1)解:∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,
∴AC=DC,∠A=60°,
∴△ADC是等边三角形,
∴∠ACD=60°,
∴n的值是60
(2)解:四边形ACFD是菱形;
理由:∵∠DCE=∠ACB=90°,F是DE的中点,
∴FC=DF=FE,
∵∠CDF=∠A=60°,
∴△DFC是等边三角形,
∴DF=DC=FC,
∵△ADC是等边三角形,
∴AD=AC=DC,
∴AD=AC=FC=DF,
∴四边形ACFD是菱形
【解析】(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 .
,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 . 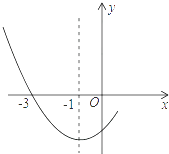
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.
(1)购买一支钢笔和一本笔记本各需多少钱?
(2)若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交
轴交 ![]() 、
、 ![]() 两点,直线
两点,直线 ![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.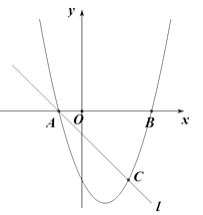
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 ![]() 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( ) 
A.121
B.362
C.364
D.729
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究: 如图,直线![]() 的表达式为
的表达式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的表达式;
的表达式;
(3)求![]() 的值;
的值;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出点
?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015攀枝花)某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市一次性购进两种商品共80件,且恰好用去1600元,问购进甲、乙两种商品各多少件?
(2)若该超市要使两种商品共80件的购进费用不超过1640元,且总利润(利润=售价﹣进价)不少于600元.请你帮助该超市设计相应的进货方案,并指出使该超市利润最大的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中第九卷《勾股》主要讲述了以测量问题为中心的直角三角形三边互求,之中记载了一道有趣的“引葭赴岸”问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”
译文:“今有正方形水池边长为1丈,有棵芦苇生长在它长出水面的部分为1尺.将芦苇的中央,向池岸牵引,恰好与水岸齐接.问水深,芦苇的长度分别是多少尺?”(备注:1丈=10尺)
如果设水深为![]() 尺,那么芦苇长用含
尺,那么芦苇长用含![]() 的代数式可表示为_______尺,根据题意,可列方程为______________.
的代数式可表示为_______尺,根据题意,可列方程为______________.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com