Question

【题目】如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（ ，y2）是抛物线上两点，则y1＞y2 ． 其中说法正确的是 ．

Answer 1

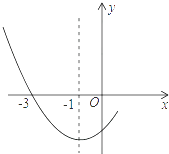
【答案】①②④
【解析】解：①∵二次函数的图象开口向上，
∴a＞0，
∵二次函数的图象交y轴的负半轴于一点，
∴c＜0，
∵对称轴是直线x=﹣1，
∴﹣ =﹣1，
∴b=2a＞0，
∴abc＜0，
故①正确；
②∵b=2a，
∴2a﹣b=0，
故②正确；
③∵抛物线的对称轴为x=﹣1，且过点（﹣3，0），
∴抛物线与x轴另一交点为（1，0）．
∵当x＞﹣1时，y随x的增大而增大，
∴当x=2时y＞0，即4a+2b+c＞0，
故③错误；
④∵（﹣5，y1）关于直线x=﹣1的对称点的坐标是（3，y1），
又∵当x＞﹣1时，y随x的增大而增大，3＞ ，
∴y1＞y2 ，
故④正确；
故答案为：①②④．
根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a-b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=-2时，y＜0，则得到4a-2b+c＜0，则可对③进行判断；通过点（-5，y1）和点（2，y2）离对称轴的远近对④进行判断．