
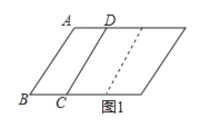
【题目】如图1,已知直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,且AB//CD,若
上,且AB//CD,若![]() 保持不动,线段
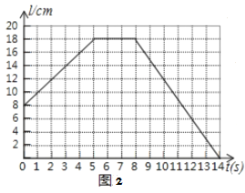
保持不动,线段![]() 先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了
先向右匀速平行移动,中间停止一段时间后再向左匀速平行移动.图2反映了![]() 的长度
的长度![]() 随时间
随时间![]() 的变化而变化的情况,则
的变化而变化的情况,则
(1)在线段![]() 开始平移之前,
开始平移之前,![]() _______
_______![]() ;
;
(2)线段![]() 边向右平移了_______
边向右平移了_______![]() ,向右平移的速度是______
,向右平移的速度是______![]() ;
;
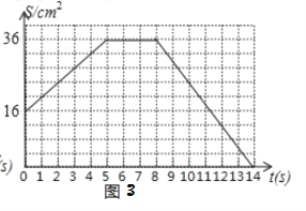
(3)图3反映了变化过程中![]() 的面积
的面积![]() 随时间
随时间![]() 变化的情况.
变化的情况.
①平行线![]() ,
,![]() 之间的距离为_______
之间的距离为_______![]() ;
;
②当![]() 时,面积S的值为_____
时,面积S的值为_____![]() ;
;
③当![]() 时,直接写出
时,直接写出![]() 关于
关于![]() 的函数关系式______(可以不化简).
的函数关系式______(可以不化简).
【答案】(1)8;(2)5,2;(3)①4;②24;③S=-6t+84(8≤t≤14).
【解析】
(1)根据CD从t=0时开始平移,在图2中找出对应的L的值即可得BC的长;
(2)由图2可得线段CD平移5s时BC的长增加了10cm,可得到中间停止时的平移距离,根据速度=距离÷时间即可得平移速度;
(3)①设m、n之间的距离为x,由图2、图3可知BC=8时,△ABC的面积为16,根据三角形的面积公式即可求出x的值,可得答案;
②由题2可知t=2时,BC=12,利用三角形面积公式即可求出S的值;
③由图2可知向左平移的距离为18cm,可求出平移速度,根据平移时间为(t-8)s,利用三角形面积公式即可得答案.
(1)∵CD开始平移时,t=0,
∴由图2可知:t=0时,L=8,
∴在线段![]() 开始平移之前,
开始平移之前,![]() 8cm,
8cm,
故答案为:8
(2)∵t为5到8s时,L的长不变,
∴CD运动到5s时停止,即CD向右平移了5s,
∵t=5时,L=18,
∴CD平移的距离为18-8=10cm,
∴CD向右平移的速度为10÷5=2cm/s,
故答案为:5,2
(3)①设m、n之间的距离为xcm,
由图2和图3可知:CD平移前BC=8,S=16,
∴S=![]() BC·x=16,
BC·x=16,
解得:x=4,即m、n之间的距离为4cm,
故答案为:4
②由图2可知:t=2时,BC=12,
∴S=![]() ×4BC=
×4BC=![]() ×4×12=24cm2,
×4×12=24cm2,
故答案为:24
③由图2、图3可知,向左平移的距离为18cm,平移的时间为6s,
∴向左平移的速度为18÷6=3cm/s,
∴S=![]() ×[18-3(t-8)]×4=-6t+84(8≤t≤14).
×[18-3(t-8)]×4=-6t+84(8≤t≤14).
故答案为:S=-6t+84(8≤t≤14)


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,A和C都在对称轴上.
(1)△ABC以直线a为对称轴作△AB1C;
(2)若∠BAC=30°,则∠BAB1=______°;
(3)求△ABB1的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
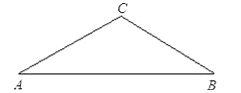
【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区集体门票的收费标准是30人以内(含30人),每人25元;超过30人,超过部分每人10元.
(1)写出应收门票费![]() (元)与游览人数
(元)与游览人数![]() (人)之间的函数关系式;
(人)之间的函数关系式;
(2)利用(1)中的函数关系式计算,某班54人去该风景区旅游时,为购门票共花了多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
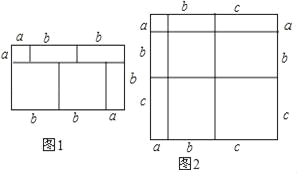
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1,可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形、3张边长为b的正方形、5张边长为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,求9x+10y+6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为菱形
为菱形![]() 对角线的交点,
对角线的交点,![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() ,
,![]() ,
,![]() 都不重合),过点
都不重合),过点![]() ,
,![]() 分别向直线
分别向直线![]() 作垂线段,垂足分别为
作垂线段,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
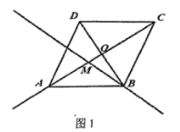
(1)①当点![]() 在线段
在线段![]() 上时,在图1中依据题意补全图形:
上时,在图1中依据题意补全图形:
②猜想![]() 与
与![]() 的数量关系为 .
的数量关系为 .
(2)小东通过观察、实验发现点![]() 在线段
在线段![]() 的延长线上运动时,(1)中的猜想始终成立.
的延长线上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明此猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与![]() 全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组![]() 和
和![]() ,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以
,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以![]() 和
和![]() 为对应边的全等三角形,即可证明猜想.
为对应边的全等三角形,即可证明猜想.
…
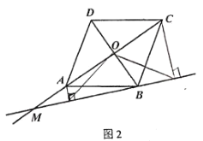
请你参考上面的想法,在图2中帮助小东完成画图,并证明此猜想(一种方法即可).
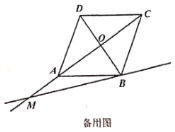
(3)当![]() 时,请直接写出线段
时,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系是 .
之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若租用甲、乙两车各运12趟需支付运费4800元,且乙车每趟运费比甲车少200元.求单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与点D对应).
(1)直接写出C,D两点的坐标;
(2)点P在x轴上,当△PCD的周长最小时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com