Question

【题目】如图1，四边形ABCD为菱形，E为对角线AC上的一个动点，连接DE并延长交射线AB于点F，连接BE．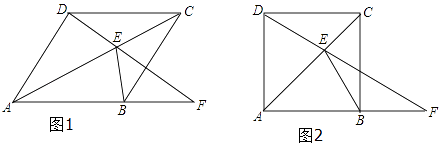
（1）求证：∠F=∠EBC；
（2）若∠DAB=90°，当△BEF为等腰三角形时，求∠F的度数（如图2）．

Answer 1

【答案】
（1）证明：∵四边形ABCD是菱形，

∴CD=AB，∠ACD=∠ACB，

在△DCE和△BCE中，

，

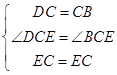∴△DCE≌△BCE（SAS），

∴∠CDE=∠CBE，

∵CD∥AB，

∴∠CDE=∠AFD，

∴∠EBC=∠AFD，即∠F=∠EBC；

（2）解：分两种情况：

①如图1，当F在AB延长线上时，

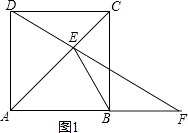
∵∠EBF为钝角，

∴只能是BE=BF，

设∠BEF=∠BFE=x°，

可通过三角形内角形为180°得：90+x+x+x=180，

解得：x=30，

∴∠EFB=30°；

②如图2，当F在线段AB上时，

∵∠EFB为钝角，

∴只能是FE=FB，设∠BEF=∠EBF=x°，则有∠AFD=2x°，

可证得：∠AFD=∠FDC=∠CBE，

得x+2x=90，

解得：x=30，

∴∠EFB=120°．

综上：∠F=30°或120°．

【解析】（1）直接利用全等三角形的判定方法得出△DCE≌△BCE（SAS），即可得出答案；（2）利用正方形的性质结合等腰三角形的性质得出：①当F在AB延长线上时；②当F在线段AB上时；分别求出即可．