【题目】如图，四边形ABCD中， BA=BC， DA=DC，我们把这种两组邻边分别相等的四边形叫做“筝形”， 其对角线AC、BD交于点M，请你猜想关于筝形的对角线的一条性质，并加以证明.
猜想：
证明：
中考解读考点精练系列答案科目：初中数学 来源： 题型：
【题目】一枚均匀的正方体骰子，六个面分别标有数字：1，2，3，4，5，6．如果用小刚抛掷正方体骰子朝上的数字x，小强抛掷正方体骰子朝上的数字y来确定点P（x，y），那么他们各抛掷一次所确定的点P落在已知直线y=﹣2x+7图象上的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，己知，A(0, 4),B (t,0)分别在y轴,x轴上，连接AB,以AB为直角边分别作等腰Rt△ABD和等腰Rt△ABC.直线BC交y轴于点E. 点G(-2,3)、H(-2,1)在第二象限内.
(1)当t =-3时，求点D的坐标.
(2)若点G、H位于直线AB的异侧，确定t的取值范围.
(3)①当t取何值时，△ABE与△ACE的面积相等.
②在①的条件下，在x轴上是否存在点P,使△PCB为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
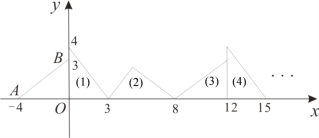
【题目】如图所示，在平面直角坐标系中，已知点A(－4，0)、B(0，3)，对△AOB连续作旋转变换可以依次得到三角形（1）、（2）、（3）、（4）、…
请你仔细观察图形，并解决以下问题：
（1）第（2）个三角形的直角顶点坐标是 ；
（2）第（5）个三角形的直角顶点坐标是 ；
（3）第（2018）个三角形的直角顶点坐标是 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在等腰Rt△ABC中，∠BAC=90°，点E在AC上（且不与点A、C重合）．在△ABC的外部作等腰Rt△CED，使∠CED=90°，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
（1）求证：△AEF是等腰直角三角形；
（2）如图2，将△CED绕点C逆时针旋转，当点E在线段BC上时，连接AE，求证：AF=
AE；
（3）如图3，将△CED绕点C继续逆时针旋转，当平行四边形ABFD为菱形，且△CED在△ABC的下方时，若AB=2
，CE=2，求线段AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小李从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子，且此长方体箱子的底面长比宽多2m，现己知购买这种铁皮每平方米需30元钱，问小李购回这张矩形铁皮共花了多少元钱?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，直线
与抛物线
交于不同的两点
、
(点在点的左侧).
（1）直接写出的坐标 ； (用
的代数式表示)
（2）设抛物线的顶点为
，对称轴
与直线的交点为
，连结
、
，若S△NDC=3×S△MDC，求抛物线的解析式;
（3）如图②，在(2)的条件下，设该抛物线与
轴交于
、
两点，点
为直线
下方抛物线上一动点，连接
、
，设直线
交线段于点
，△MPQ的面积为
，△MAQ的面积为
，求
的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
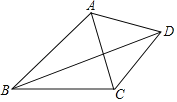
【题目】如图，已知：四边形ABCD中，对角线BD平分∠ABC，∠ACB＝74°，∠ABC＝46°，且∠BAD+∠CAD＝180°，那么∠BDC的度数为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
