
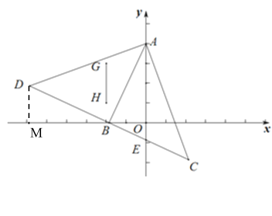
【题目】如图,己知,A(0, 4),B (t,0)分别在y轴,x轴上,连接AB,以AB为直角边分别作等腰Rt△ABD和等腰Rt△ABC.直线BC交y轴于点E. 点G(-2,3)、H(-2,1)在第二象限内.

(1)当t =-3时,求点D的坐标.
(2)若点G、H位于直线AB的异侧,确定t的取值范围.
(3)①当t取何值时,△ABE与△ACE的面积相等.
②在①的条件下,在x轴上是否存在点P,使△PCB为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
【答案】(1)D(-7,3);(2)![]() ;(3)①-2;②存在,P(6,0),P(
;(3)①-2;②存在,P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0)
-2,0)
【解析】
(1)当t=-3时,过点D作DM⊥x轴于点M,证明△ABO≌△BDM,得出DM=BO和MB=OA,从而得出点D坐标.
(2)设出AB解析式y=kx+4,分别求出点G,H在线段AB上的时点B的坐标;
(3)①假设△ABE与△ACE的面积相等,利用等底同高求出t值;
②根据等腰三角形的性质,分BP=BC、CP=CB、PC=PB三种情况讨论.
(1)当t=-3时,过点D作DM⊥x轴于点M,
∵△ABD为等腰直角三角形,AB=BD,∠ABD=90°
∴∠ABO+∠DBM=180°-90°=90°
又∵DM⊥x轴于点M
∴∠DMB=90°
∴∠DBM+∠MDB=90°
∴∠MDB=∠ABO
在△ABO和△BDM中

∴△ABO≌△BDM
∴DM=BO=3,MB=OA=4
∴MO=MB+BO=4+3=7
∴D(-7,3)
(2)∵A(0,4),B(t,0),设直线AB的解析式为y=kx+4
当点G(-2,3)在直线AB上时
3=-2k+4,![]()
此时AB的解析式![]()
当y=0时,![]() ,x=-8
,x=-8
此时B(-8,0)
当点H(-2,1)在直线AB上时
1=-2k+4,![]()
此时AB的解析式![]()
当y=0时,![]() ,x=
,x=![]()
此时B(![]() ,0)
,0)
∵点G, H位于直线AB的异侧,
∴由图像可知直线AB与线段MN相交,且点M,N不在直线AB上
∴![]()
(3)①t=-2时,△ABE与△ACE的面积相等.
如图,过点B做x轴垂线,构造直角三角形ARB和直角三角形BQC,
∵∠RAB+∠ABR=90°,∠ABR+∠BCQ=90°
∴∠ABR=∠BCQ,
在△ARB和△BQC中,
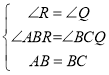 ,
,
∴△ARB≌△BQC(AAS)
∴AR=BQ,BR=QC=4,
若△ABE与△ACE的面积相等,
则BE=EC,
∴BO=CN=2,
∴B(-2,0)

②P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0)
-2,0)
由②可得C(2,-2)
当BP=BC时,
BC=![]() =
=![]() ,
,
∴BP=![]()
∴P(-2![]() -2,0)或P(2
-2,0)或P(2![]() -2,0)
-2,0)
当CP=CB时,
BP=8,
∴P(6,0)
当PC=PB时,
如图,过E作BC的垂线,交x轴于点P,过C作x轴垂线于点S,
设BP=m=PC,则PS=4-m,
在△PSC中,PS2+SC2=PC2,
即22+(4- m)2= m 2,
解得m=![]() ,
,
∴OP=![]() -2=
-2=![]() ,
,
∴P(![]() ,0).
,0).
综上:P(6,0),P(![]() ,0),P(-2
,0),P(-2![]() -2,0),P(2
-2,0),P(2![]() -2,0).
-2,0).


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
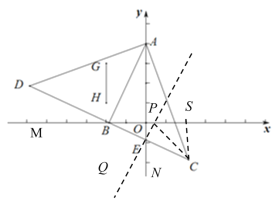
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°.

(1)尺规作图:作AB的垂直平分线MN交AC于点D,连接BD;(保留作图痕迹,不写作法)
(2)求∠DBC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.下面我们依次对![]() 展开式的各项系数进一步研究发现,当
展开式的各项系数进一步研究发现,当![]() 取正整数时可以单独列成表中的形式:
取正整数时可以单独列成表中的形式:
例如,在三角形中第二行的三个数1,2,1,恰好对应![]() 展开式中的系数,
展开式中的系数,

(1)根据表中规律,写出![]() 的展开式;
的展开式;
(2)多项式![]() 的展开式是一个几次几项式?并预测第三项的系数;
的展开式是一个几次几项式?并预测第三项的系数;
(3)请你猜想多项式![]() 取正整数)的展开式的各项系数之和(结果用含字母
取正整数)的展开式的各项系数之和(结果用含字母![]() 的代数式表示);
的代数式表示);
(4)利用表中规律计算:![]() (不用表中规律计算不给分).
(不用表中规律计算不给分).
查看答案和解析>>
科目:初中数学 来源: 题型:
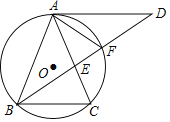
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于国家对农业的大力扶持,农民的种粮积极性得到极大提高.国家统计局提供的数据表明,我国粮食产量连续两年大幅增长,![]() 年粮食产量为
年粮食产量为![]() 亿斤,
亿斤,![]() 年达到了
年达到了![]() 亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为
亿斤,若要求这两年粮食产量的平均增长率,可设平均增长率为![]() ,列方程为________.
,列方程为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中, BA=BC, DA=DC,我们把这种两组邻边分别相等的四边形叫做“筝形”, 其对角线AC、BD交于点M,请你猜想关于筝形的对角线的一条性质,并加以证明.
猜想:
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.

(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF=![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com