练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一枚均匀的正方体骰子，六个面分别标有数字：1，2，3，4，5，6．如果用小刚抛掷正方体骰子朝上的数字x，小强抛掷正方体骰子朝上的数字y来确定点P（x，y），那么他们各抛掷一次所确定的点P落在已知直线y=﹣2x+7图象上的概率是多少？

    【答案】；

    【解析】

    根据概率的求法，找准两点：
    ①符合条件的情况数目；
    ②全部情况的总数．
    二者的比值就是其发生的概率．

    由题意可得1≤﹣2x+7≤6，化为不等式组解得≤x≤3.1≤x≤6，且x为正整数，

    ∴x=1，2，3．要使点P落在直线y=﹣2x+7图象上，则对应的y=5，3，1，

    ∴满足条件的点P有（1，5），（2，3），（3，1）抛掷骰子所得P点的总个数为36，

    ∴点P落在直线y=﹣2x+7图象上的概率P==，

    答：点P落在直线y=﹣2x+7图象上的概率是．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在边AB上有一点（点不与点、点重合），过点作直线截，使截得的三角形与相似，满足条件的直线共有（ ）

    A. 2条 B. 3条 C. 4条 D. 5条

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=AC，∠A=36°．

    （1）尺规作图：作AB的垂直平分线MN交AC于点D，连接BD；（保留作图痕迹，不写作法）

    （2）求∠DBC的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O′在第一象限，⊙O′与x轴相切于H点，与y轴相交于A（0，2），B（0，8），则点O′的坐标是（　　）

    A. （6，4） B. （4，6） C. （5，4） D. （4，5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

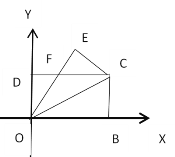
    【题目】如图，长方形OBCD的OB边在x轴上，OD在y轴上，把OBC沿OC折叠得到OCE，OE与CD交于点F.

    （１）求证：OF＝CF；

    （２）若OD＝４，OB＝８，写出OE所在直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A—B—C—D回到点A，设点P的运动时间为t秒。

    （1）当t=3秒时，求△ABP的面积；

    （2）当t为何值时，点P与点A的距离为5cm？

    （3）当t为何值时（2＜t＜5），以线段AD、CP、AP的长度为三角形是直角三角形，且AP是斜边。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例.下面我们依次对展开式的各项系数进一步研究发现，当取正整数时可以单独列成表中的形式：

    例如，在三角形中第二行的三个数1，2，1，恰好对应展开式中的系数，

    (1)根据表中规律，写出的展开式；

    (2)多项式的展开式是一个几次几项式？并预测第三项的系数；

    (3)请你猜想多项式取正整数）的展开式的各项系数之和（结果用含字母的代数式表示）；

    (4)利用表中规律计算：（不用表中规律计算不给分）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

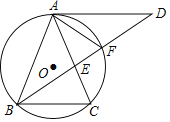
    【题目】如图，△ABC内接于⊙O，AB=AC，∠BAC=36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F．

    （1）求∠DAF的度数；

    （2）求证：AE2=EFED；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中， BA=BC， DA=DC，我们把这种两组邻边分别相等的四边形叫做“筝形”， 其对角线AC、BD交于点M，请你猜想关于筝形的对角线的一条性质，并加以证明.

    猜想：

    证明：

    查看答案和解析>>

    同步练习册答案