
【题目】在![]() 边AB上有一点
边AB上有一点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合),过点
重合),过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,满足条件的直线共有( )
相似,满足条件的直线共有( )
A. 2条 B. 3条 C. 4条 D. 5条
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克的西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完,销售金额与西瓜的千克数之间的关系如图所示,那么小李赚了( )
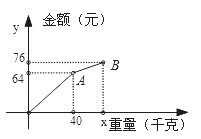
A. 32元B. 36元C. 38元D. 44元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以直线x=![]() 对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y轴交于C(0,5),直线l与y轴交于点D.
(1)求抛物线的函数表达式;
(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD面积相等,求点G的坐标;
,且△BCG与△BCD面积相等,求点G的坐标;
(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
“最短路径问题”是数学中一类具有挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.有一天,一位将军向他请教一个问题:如图1,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为使马走的路程最短,应该让马在什么地方饮水?
海伦认为以河边为镜面,画出甲地的镜像点(垂直河边的等距离点),然后连接乙地和甲地的镜像点,会跟河边相交一点,这个点就是马饮水的地方,马走的路程最短(两点之间直线距离最短).

任务:
(1)请你帮海伦在图1的位置完成作图,并标出马饮水的地点![]() (画出草图即可);
(画出草图即可);
(2)如图2,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .请你在
.请你在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小,并直接写出点
最小,并直接写出点![]() 的坐标(保留作图痕迹);
的坐标(保留作图痕迹);

应用:
(3)如图3,圆柱形容器高为![]() ,底面周长为
,底面周长为![]() ,在杯内壁离杯底
,在杯内壁离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 处的点
处的点![]() 处,点
处,点![]() 与
与![]() 的水平距离等于底面直径,求蚂蚁从外壁
的水平距离等于底面直径,求蚂蚁从外壁![]() 处到达内壁
处到达内壁![]() 处的最短距离.
处的最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市2019年11月21日---11月27日最高气温走势图,则下列说法不正确的是( )

A.21日---22日的最高气温呈上升趋势
B.这7天中,23日的最高气温高于其他6天的的最高气温
C.23---25日的最高气温呈下降趋势
D.相邻两天中,24日---25日的最高气温变化最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,D,E分别在AB,AC上,AD=AE,将△ADE绕点A逆时针任意旋转.

(1)发现:如图2,连结BD,CE,若∠BAC=60°,D点恰在线段BE上,则∠BEC= °;
(2)探究:如图3,连结BD,CE,并交于点F,求证:∠BFC=∠BAC;
(3)拓展:如图4,若∠BAC=90°,AB=5,AD=2,连结CD,BE,请直接写出四边形BCDE的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
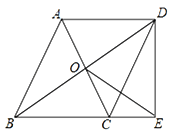
【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚均匀的正方体骰子,六个面分别标有数字:1,2,3,4,5,6.如果用小刚抛掷正方体骰子朝上的数字x,小强抛掷正方体骰子朝上的数字y来确定点P(x,y),那么他们各抛掷一次所确定的点P落在已知直线y=﹣2x+7图象上的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com