
ЁОЬтФПЁПдФЖСЯТСаВФСЯВЂЭъГЩШЮЮёЃК
ЁАзюЖЬТЗОЖЮЪЬтЁБЪЧЪ§бЇжавЛРрОпгаЬєеНадЕФЮЪЬт.ЦфЪЕЃЌЪ§бЇЪЗЩЯвВгаВЛЩйЯрЙиЕФЙЪЪТЃЌШчЯТМДЮЊЦфжаНЯЮЊОЕфЕФвЛдђЃКЙХЯЃРАгавЛЮЛОУИКЪЂУћЕФбЇепЃЌУћНаКЃТз.ЫћОЋЭЈЪ§бЇЁЂЮяРэЃЌДЯЛлЙ§ШЫ.гавЛЬьЃЌвЛЮЛНЋОќЯђЫћЧыНЬвЛИіЮЪЬтЃКШчЭМ1ЃЌНЋОќДгМзЕиЦяТэГіЗЂЃЌвЊЕНКгБпШУТэвћЫЎЃЌШЛКѓдйЛиЕНввЕиЕФТэХяЃЌЮЊЪЙТэзпЕФТЗГЬзюЖЬЃЌгІИУШУТэдкЪВУДЕиЗНвћЫЎЃП
КЃТзШЯЮЊвдКгБпЮЊОЕУцЃЌЛГіМзЕиЕФОЕЯёЕуЃЈДЙжБКгБпЕФЕШОрРыЕуЃЉЃЌШЛКѓСЌНгввЕиКЭМзЕиЕФОЕЯёЕуЃЌЛсИњКгБпЯрНЛвЛЕуЃЌетИіЕуОЭЪЧТэвћЫЎЕФЕиЗНЃЌТэзпЕФТЗГЬзюЖЬЃЈСНЕужЎМфжБЯпОрРызюЖЬЃЉ.

ШЮЮёЃК
ЃЈ1ЃЉЧыФуАяКЃТздкЭМ1ЕФЮЛжУЭъГЩзїЭМЃЌВЂБъГіТэвћЫЎЕФЕиЕу![]() ЃЈЛГіВнЭММДПЩЃЉЃЛ
ЃЈЛГіВнЭММДПЩЃЉЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ
ЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .ЧыФудк
.ЧыФудк![]() жсЩЯеввЛЕу
жсЩЯеввЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() зюаЁЃЌВЂжБНгаДГіЕу
зюаЁЃЌВЂжБНгаДГіЕу![]() ЕФзјБъЃЈБЃСєзїЭМКлМЃЃЉЃЛ
ЕФзјБъЃЈБЃСєзїЭМКлМЃЃЉЃЛ

гІгУЃК
ЃЈ3ЃЉШчЭМ3ЃЌдВжљаЮШнЦїИпЮЊ![]() ЃЌЕзУцжмГЄЮЊ
ЃЌЕзУцжмГЄЮЊ![]() ЃЌдкБФкБкРыБЕз
ЃЌдкБФкБкРыБЕз![]() ЕФЕу
ЕФЕу![]() ДІгавЛЕЮЗфУлЃЌДЫЪБвЛжЛТьвЯе§КУдкБЭтБкЃЌРыБЩЯби
ДІгавЛЕЮЗфУлЃЌДЫЪБвЛжЛТьвЯе§КУдкБЭтБкЃЌРыБЩЯби![]() ДІЕФЕу
ДІЕФЕу![]() ДІЃЌЕу
ДІЃЌЕу![]() гы
гы![]() ЕФЫЎЦНОрРыЕШгкЕзУцжБОЖЃЌЧѓТьвЯДгЭтБк
ЕФЫЎЦНОрРыЕШгкЕзУцжБОЖЃЌЧѓТьвЯДгЭтБк![]() ДІЕНДяФкБк
ДІЕНДяФкБк![]() ДІЕФзюЖЬОрРы.
ДІЕФзюЖЬОрРы.

ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЭМЯъМћНтЮіЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛЃЈ3ЃЉТьвЯДгЭтБк
ЃЛЃЈ3ЃЉТьвЯДгЭтБк![]() ДІЕНДяФкБк
ДІЕНДяФкБк![]() ДІЕФзюЖЬОрРыЮЊ
ДІЕФзюЖЬОрРыЮЊ![]() .
.
ЁОНтЮіЁП
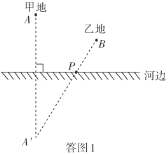
ЃЈ1ЃЉИљОндкКгБпЩЯЕФЭЌВргаСНИіЕуAЁЂBЃЌдкжБЯпLЩЯгаЕНAЁЂBЕФОрРыжЎКЭзюЖЬЕФЕуДцдкЃЌПЩвдЭЈЙ§жсЖдГЦРДШЗЖЈЃЌМДзїГіЦфжавЛЕуЙигкжБЯпlЕФЖдГЦЕуЃЌЖдГЦЕугыСэвЛЕуЕФСЌЯпгыКгБпЯпЕФНЛЕуОЭЪЧЫљвЊевЕФЕуЃЎ
ЃЈ2ЃЉевГіCЕФЖдГЦЕуCЁфЃЌСЌНгBCЁфЃЌгыxжсНЛЕуМДЮЊQЃЛ
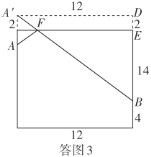
ЃЈ3ЃЉНЋБзгВрУцеЙПЊЃЌНЈСЂAЙигкEFЕФЖдГЦЕуAЁфЃЌИљОнСНЕужЎМфЯпЖЮзюЖЬПЩжЊAЁфBЕФГЄЖШМДЮЊЫљЧѓЃЎ
НтЃКЃЈ1ЃЉШчД№ЭМ1МДЮЊЫљзїЭМаЮ.
ЃЈ2ЃЉШчД№ЭМ2ЃЌЕу![]() МДЮЊЫљЧѓ.
МДЮЊЫљЧѓ.
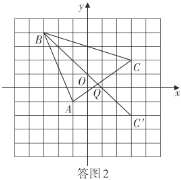
Еу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]()
ЃЈ3ЃЉШчД№ЭМ3ЪЧБзгЕФВрУцЕФВПЗжеЙПЊЭМЃЌ
ЩшЕу![]() ЮЊБзгВрУцеЙПЊЭМЩЯБпбиЕФжаЕуЃЌзїЕу
ЮЊБзгВрУцеЙПЊЭМЩЯБпбиЕФжаЕуЃЌзїЕу![]() ЙигкЩЯБпбиЕФЖдГЦЕу
ЙигкЩЯБпбиЕФЖдГЦЕу![]() ЃЌ
ЃЌ
СЌНг![]() ЃЌдђ
ЃЌдђ![]() МДЮЊзюЖЬОрРыЃЌ
МДЮЊзюЖЬОрРыЃЌ
Щш![]() гыеЙПЊЭМЕФЩЯБпдЕНЛгкЕу
гыеЙПЊЭМЕФЩЯБпдЕНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌЧвгы
ЃЌЧвгы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
![]() .
.
дк![]() жаЃЌ
жаЃЌ
![]() .
.
ЁрТьвЯДгЭтБк![]() ДІЕНДяФкБк
ДІЕНДяФкБк![]() ДІЕФзюЖЬОрРыЮЊ
ДІЕФзюЖЬОрРыЮЊ![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЁїABCЕФЖЅЕуОљдкИёЕуЩЯЃЌЕуCЕФзјБъЮЊЃЈ4ЃЌ-1ЃЉЃЎ
ЃЈ1ЃЉЧывдyжсЮЊЖдГЦжсЃЌЛГігыЁїABCЖдГЦЕФЁїA1B1C1ЃЌВЂжБНгаДГіЕуA1ЁЂB1ЁЂC1ЕФзјБъЃЛ
ЃЈ2ЃЉЁїABCЕФУцЛ§ЪЧ ЃЎ
ЃЈ3ЃЉЕуPЃЈa+1ЃЌb-1ЃЉгыЕуCЙигкxжсЖдГЦЃЌдђa= ЃЌb= ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁЛЊЭЌбЇЯыВтСПбЇаЃвнЗђТЅЕФИпЖШЃЌЫћеОдкBЕуДгAДІбіЭћТЅЖЅDЃЌВтЕУбіНЧЮЊ30ЁуЃЌдйЭљвнЗђТЅЕФЗНЯђЧАНј14УзДгEДІЭћТЅЖЅЃЌВтЕУбіНЧЮЊ60ЁуЃЌвбжЊаЁЛЊЭЌбЇЩэИпЃЈABЃЉЮЊ1.6УзЃЌдђвнЗђТЅCDЕФИпЖШЕФЮЊЃЈЁЁЁЁЃЉЃЈ![]() Ёж1.73ЃЉ
Ёж1.73ЃЉ

A.12.1УзB.13.7УзC.11.5УзD.13.5Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓОЙ§ЕуЃЈЉ1ЃЌЉ2
ЕФЭМЯѓОЙ§ЕуЃЈЉ1ЃЌЉ2![]() ЃЉЃЌЕуAЪЧИУЭМЯѓЕквЛЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮABCЃЌЖЅЕуCдкЕкЫФЯѓЯоЃЌACгыxжсНЛгкЕуDЃЌЕБ
ЃЉЃЌЕуAЪЧИУЭМЯѓЕквЛЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮABCЃЌЖЅЕуCдкЕкЫФЯѓЯоЃЌACгыxжсНЛгкЕуDЃЌЕБ![]() ЪБЃЌдђЕуCЕФзјБъЮЊ______ЃЎ
ЪБЃЌдђЕуCЕФзјБъЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
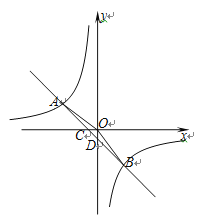
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ4ЃЉЃЌСЌНгAOЃЌAO=5ЃЌsinЁЯAOC=
ЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЃЌBСНЕуЃЌгыxжсНЛгкЕуCЃЌгыyжсНЛгкЕуDЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ4ЃЉЃЌСЌНгAOЃЌAO=5ЃЌsinЁЯAOC=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪН
ЃЈ2ЃЉСЌНгOBЃЌЧѓЁїAOBЕФУцЛ§
(3) ИљОнЭМЯѓжБНгаДГіЕБ![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() БпABЩЯгавЛЕу
БпABЩЯгавЛЕу![]() ЃЈЕу
ЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() ЁЂЕу
ЁЂЕу![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зїжБЯпНи
зїжБЯпНи![]() ЃЌЪЙНиЕУЕФШ§НЧаЮгы
ЃЌЪЙНиЕУЕФШ§НЧаЮгы![]() ЯрЫЦЃЌТњзуЬѕМўЕФжБЯпЙВгаЃЈ ЃЉ
ЯрЫЦЃЌТњзуЬѕМўЕФжБЯпЙВгаЃЈ ЃЉ
A. 2Ьѕ B. 3Ьѕ C. 4Ьѕ D. 5Ьѕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЦНааЫФБпаЮжНЦЌ![]() АДШчЭМЗНЪНелЕўЃЌЪЙЕу
АДШчЭМЗНЪНелЕўЃЌЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЃЌЕу
жиКЯЃЌЕу![]() ЕФТфЕуМЧЮЊЕу
ЕФТфЕуМЧЮЊЕу![]() ЃЌелКлЮЊ
ЃЌелКлЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ

![]() ЧѓжЄЃКЫФБпаЮ
ЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
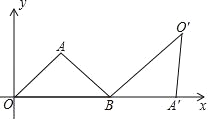
ЁОЬтФПЁПШчЭМЃЌЕуAЕФзјБъЮЊЃЈ3ЃЌ![]() ЃЉЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌНЋЁїAOBШЦЕуBАДЫГЪБеыЗНЯђа§зЊвЛЖЈЕФНЧЖШКѓЕУЕНЁїAЁфOЁфBЃЌЕуAЕФЖдгІЕуAЁфдкxжсЩЯЃЌдђЕуOЁфЕФзјБъЮЊ_____ЃЎ
ЃЉЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЌНЋЁїAOBШЦЕуBАДЫГЪБеыЗНЯђа§зЊвЛЖЈЕФНЧЖШКѓЕУЕНЁїAЁфOЁфBЃЌЕуAЕФЖдгІЕуAЁфдкxжсЩЯЃЌдђЕуOЁфЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌГЄЗНаЮOBCDЕФOBБпдкxжсЩЯЃЌODдкyжсЩЯЃЌАбOBCбиOCелЕўЕУЕНOCEЃЌOEгыCDНЛгкЕуF.
ЃЈЃБЃЉЧѓжЄЃКOFЃНCFЃЛ
ЃЈЃВЃЉШєODЃНЃДЃЌOBЃНЃИЃЌаДГіOEЫљдкжБЯпЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com