
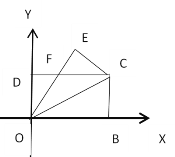
【题目】如图,长方形OBCD的OB边在x轴上,OD在y轴上,把OBC沿OC折叠得到OCE,OE与CD交于点F.
(1)求证:OF=CF;
(2)若OD=4,OB=8,写出OE所在直线的解析式.
【答案】(1)证明见解析;(2)y=![]() x.
x.
【解析】
(1)根据平行的性质和轴对称的性质,可得∠BOC=∠FOC=∠FCO,即可证得;
(2)可设FC=x=OF,则DF=8-x,则在直角△ODF中,根据勾股定理,可求出x,即可得出DF的长,从而可求出F点的坐标,再用待定系数法求出OE所在直线的解析式.
(1)证明:∵四边形OBCD是长方形 ∴∠BOC=∠OCD
∵OBC折叠成OCE ∴∠BOC=∠EOC
∴∠EOC=∠OCD ∴OF=CF
(2)设FC=x,则(8-x)2+42=x2 解得:x=5, ∴ DF=8-5=3, ∴点F的坐标为;(3,4)
设OE所在直线方程为y=kx,
把(3,4)代入y=kx,得k=![]() ,
,
OE所在直线方程为y=![]() x.
x.


科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
“最短路径问题”是数学中一类具有挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:古希腊有一位久负盛名的学者,名叫海伦.他精通数学、物理,聪慧过人.有一天,一位将军向他请教一个问题:如图1,将军从甲地骑马出发,要到河边让马饮水,然后再回到乙地的马棚,为使马走的路程最短,应该让马在什么地方饮水?
海伦认为以河边为镜面,画出甲地的镜像点(垂直河边的等距离点),然后连接乙地和甲地的镜像点,会跟河边相交一点,这个点就是马饮水的地方,马走的路程最短(两点之间直线距离最短).

任务:
(1)请你帮海伦在图1的位置完成作图,并标出马饮水的地点![]() (画出草图即可);
(画出草图即可);
(2)如图2,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .请你在
.请你在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小,并直接写出点
最小,并直接写出点![]() 的坐标(保留作图痕迹);
的坐标(保留作图痕迹);

应用:
(3)如图3,圆柱形容器高为![]() ,底面周长为
,底面周长为![]() ,在杯内壁离杯底
,在杯内壁离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 处的点
处的点![]() 处,点
处,点![]() 与
与![]() 的水平距离等于底面直径,求蚂蚁从外壁
的水平距离等于底面直径,求蚂蚁从外壁![]() 处到达内壁
处到达内壁![]() 处的最短距离.
处的最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(5,0)和点B(0,4).


(1)求直线AB所对应的函数表达式;
(2)设直线y=x与直线AB相交于点C,求△BOC的面积;
(3)若将直线OC沿x轴向右平移,交y轴于点O′,当△AB O′为等腰三角形时,直接写出点O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班男同学身高情况如下表,则其中数据167cm( )
身高(cm) | 170 | 169 | 168 | 167 | 166 | 165 | 164 | 163 |
人数(人) | 1 | 2 | 5 | 8 | 6 | 3 | 3 | 2 |
A.是平均数B.是众数但不是中位数.
C.是中位数但不是众数D.是众数也是中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚均匀的正方体骰子,六个面分别标有数字:1,2,3,4,5,6.如果用小刚抛掷正方体骰子朝上的数字x,小强抛掷正方体骰子朝上的数字y来确定点P(x,y),那么他们各抛掷一次所确定的点P落在已知直线y=﹣2x+7图象上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读数月活动中学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类)。下图是根据调查结果绘制的两幅不完整的统计图。

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中![]() ;
;
(3)扇形统计图中,艺术类读数所在扇形的圆心角是 度;
(4)学校计划购买课外读物8000册,请根据样本数据,估计学校购买其他类读数多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年,某校将开展“爱我中华,了解历史”为主题的知识竞赛,八年级某老师为了解所任教的甲,乙两班学生相关知识的掌握情况,对两个班的学生进行了中国历史知识检测,满分为100分.现从两个班分别随机抽取了20名学生的检测成绩进行整理、描述和分析,下面给出了部分信息:(成绩得分用x表示,共分为五组,A组:0≤x<80,B组:80≤x<85,C组:85≤x<90,D组:90≤x<95,E组:95≤x≤100)
甲班20名学生的成绩为:
82,85,96,73,91,99,87,91,86,91
87, 94,89, 96,96,91,100,93,94, 99
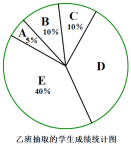
乙班20名学生的成绩在D组中的数据是:91,92,92,92,92,93,94
甲,乙两班抽取的学生成绩数据统计表:
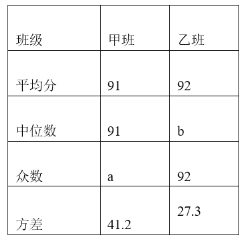
根据以上信息,解答下列问题:
(1)请直接写出上述统计表中a,b的值:a= ,b= ;
(2)若甲,乙两班总人数为120名,且都参加了此次知识检测,若规定成绩得分x≥95为优秀,请估计此次检测成绩优秀的学生人数是多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com