
【题目】某商店分两次购进A,B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
A | B | ||
第一次 | 20 | 30 | 2800 |
第二次 | 30 | 20 | 2200 |
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
【答案】(1)A、B两种商品每件的进价分别是20元,80元;(2)a=800时,m的最大值为12000元.
【解析】
(1)设A种商品每件的进价为x元,B种商品每件的进价为y元,根据两次进货情况表,可得出关于x、y的二元一次方程组,解之即可得出结论;
(2))设A商品a件,B商品(1000﹣a)件,利润为m元,根据题意列出不等式组,解之即可得出a的取值范围,根据总利润=单件利润×购进数量,可得出m和a的函数关系式,再根据一次函数的性质即可解决最值问题.
(1)设A、B两种商品每件的进价分别是x元,y元
根据题意得:![]()
解得:![]()
答A、B两种商品每件的进价分别是20元,80元.
(2)设A商品a件,B商品(1000﹣a)件,利润为m元.
根据题意得: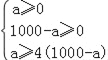
解得:800≤a≤1000
m=(30﹣20)a+(100﹣80)(1000﹣a)=20000﹣10a
∵k=﹣10<0
∴m随a的增大而减小
∴a=800时,m的最大值为12000元.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点A′的坐标(____________),顶点B的坐标(____________),顶点C关于原点对称的点C′的坐标(____________).
(2)△ABC的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:![]() =___________,
=___________,![]() =___________,
=___________,![]() =___________,
=___________,
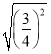 =_________,
=_________,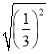 =__________,
=__________,![]() =___________,
=___________,
根据计算结果,回答:
(1)![]() 一定等于
一定等于![]() 吗?你发现其中的规律了吗?请你用数学语言描述出来。
吗?你发现其中的规律了吗?请你用数学语言描述出来。
(2)利用你总结的规律,计算:
①若![]() ,则
,则![]() =_____________;
=_____________;
②![]() =______________________;
=______________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示a,点B表示b,且a,b满足![]()
(1)x表示a+b的整数部分,y表示a+b的小数部分,则x= y = ;
(2)若点A与点C之间的距离表示AC,点B与点C之间的距离表示BC,请在数轴上找一点C,使得AC=2BC,求点C在数轴上表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.



(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com