
【题目】如图,已知双曲线![]() 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
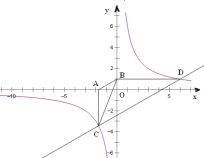
(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
【答案】(1)k=6;(2)![]() ;(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
;(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
【解析】
试题分析:(1)把点D的坐标代入双曲线解析式,进行计算即可得解;
(2)先根据点D的坐标求出BD的长度,再根据三角形的面积公式求出点C到BD的距离,然后求出点C的纵坐标,再代入反比例函数解析式求出点C的坐标,然后利用待定系数法求一次函数解析式解答;
(3)根据题意求出点A、B的坐标,然后利用待定系数法求出直线AB的解析式,可知与直线CD的解析式k值相等,所以AB、CD平行.
解:(1)∵双曲线![]() 经过点D(6,1),
经过点D(6,1),
∴![]() ,解得k=6;
,解得k=6;
(2)设点C到BD的距离为h,
∵点D的坐标为(6,1),DB⊥y轴,
∴BD=6,
∴S△BCD=![]() ×6h=12,
×6h=12,
解得h=4,
∵点C是双曲线第三象限上的动点,点D的纵坐标为1,
∴点C的纵坐标为1-4=-3,
∴![]() ,解得x=-2,
,解得x=-2,
∴点C的坐标为(-2,-3),
设直线CD的解析式为y=kx+b,

所以,直线CD的解析式为![]() ;
;
(3)AB∥CD.理由如下:
∵CA⊥x轴,DB⊥y轴,设点C的坐标为(c,![]() ),点D的坐标为(6,1),
),点D的坐标为(6,1),
∴点A、B的坐标分别为A(c,0),B(0,1),
设直线AB的解析式为y=mx+n,
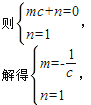
所以,直线AB的解析式为y=-![]() x+1,
x+1,
设直线CD的解析式为y=ex+f,

∴直线CD的解析式为y=-![]() x+
x+![]() ,
,
∵AB、CD的解析式k都等于-![]() ,
,
∴AB与CD的位置关系是AB∥CD.


科目:初中数学 来源: 题型:
【题目】为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
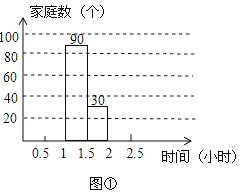
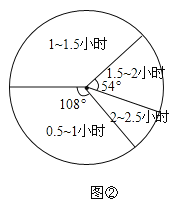
(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该玩具每天的销售利润最大;
(3)专柜结合上述情况,设计了A、B两种营销方案:
方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是()
A.43B.44C.45D.46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在边BC上,且四边形AEFD是平行四边形. 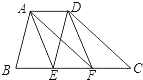
(1)AD与BC有何等量关系,请说明理由;
(2)当AB=DC时,求证:平行四边形AEFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友能分到不足5个苹果.这一箱苹果的个数是 , 小朋友的人数是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 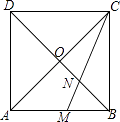
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com