
【题目】如图(1)所示,在A,B两地间有一车站C,甲汽车从A地出发经C站匀速驶往B地,乙汽车从B地出发经C站匀速驶往A地,两车速度相同.如图(2)是两辆汽车行驶时离C站的路程y(千米)与行驶时间x(小时)之间的函数关系的图象.
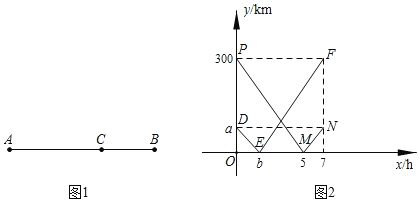
(1)填空:a= km,b= h,AB两地的距离为 km;
(2)求线段PM、MN所表示的y与x之间的函数表达式(自变量取值范围不用写);
(3)求行驶时间x满足什么条件时,甲、乙两车距离车站C的路程之和最小?
【答案】(1)120,2,420;(2)线段PM所表示的y与x之间的函数表达式是y=﹣60x+300,线段MN所表示的y与x之间的函数表达式是y=60x﹣300;(3)行驶时间x满足2≤x≤5时,甲、乙两车距离车站C的路程之和最小.
【解析】
(1)根据题意和图象中的数据,可以求得a、b的值以及AB两地之间的距离;
(2)根据(1)中的结果和函数图象中的数据,可以求得线段PM、MN所表示的y与x之间的函数表达式;
(3)根据题意,可以写出甲、乙两车距离车站C的路程之和和s之间的函数关系式,然后利用一次函数的性质即可解答本题.
(1)两车的速度为:300÷5=60km/h,
a=60×(7﹣5)=120,
b=7﹣5=2,
AB两地的距离是:300+120=420.
故答案为:120,2,420;
(2)设线段PM所表示的y与x之间的函数表达式是y=kx+b,
![]() ,得
,得![]() ,
,
即线段PM所表示的y与x之间的函数表达式是y=﹣60x+300;
设线段MN所表示的y与x之间的函数表达式是y=mx+n,
![]() ,得
,得![]() ,
,
即线段MN所表示的y与x之间的函数表达式是y=60x﹣300;
(3)设DE对应的函数解析式为y=cx+d,
![]() ,得
,得![]() ,
,
即DE对应的函数解析式为y=﹣60x+120,
设EF对应的函数解析式为y=ex+f,
![]() ,得
,得![]() ,
,
即EF对应的函数解析式为y=60x﹣120,
设甲、乙两车距离车站C的路程之和为skm,
当0≤x≤2时,
s=(﹣60x+300)+(﹣60x+120)=﹣120x+420,
则当x=2时,s取得最小值,此时s=180,
当2<x≤5时,
s=(﹣60x+300)+(60x﹣120)=180,
当5≤x≤7时,
s=(60x﹣300)+(60x﹣120)=120x﹣420,
则当x=5时,s取得最小值,此时s=180,
由上可得:
行驶时间x满足2≤x≤5时,甲、乙两车距离车站C的路程之和最小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.

已知: .
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
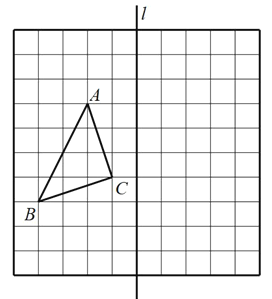
【题目】如图,点![]() 、
、![]() 、
、![]() 都在方格纸的格点上,方格纸中每个小正方形的边长都是1.
都在方格纸的格点上,方格纸中每个小正方形的边长都是1.
(1)画![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(2)在直线![]() 上找一点
上找一点![]() ,使
,使![]() 最小;(要求在直线
最小;(要求在直线![]() 上标出点
上标出点![]() 的位置)
的位置)
(3)连接![]() 、
、![]() ,计算四边形PABC的面积.
,计算四边形PABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
(1)尝试探究
如图(1),在正方形ABCD中,对角线AC、BD相交于点O,点E是BC边上一点,AE与BD交于点G,过点E作EF⊥AE交AC于点F,若![]() =2,则
=2,则![]() 的值是 ;
的值是 ;
(2)拓展迁移
如图(2),在矩形ABCD中,过点B作BH⊥AC于点O,交AD相于点H,点E是BC边上一点,AE与BH相交于点G,过点E作EF⊥AE交AC于点F.
①若∠BAE=∠ACB,sin∠EAF=![]() ,求tan∠ACB;
,求tan∠ACB;
②若![]() ,
,![]() =b(a>0,b>0),求
=b(a>0,b>0),求![]() 的值(用含a,b的代数式表示).
的值(用含a,b的代数式表示).
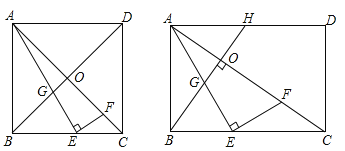
图(1) 图(2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
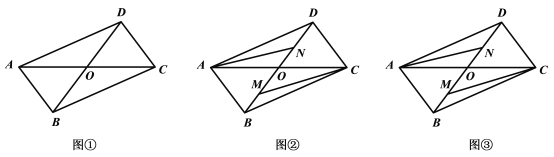
【题目】如图①所示,![]() 是某公园的平面示意图,
是某公园的平面示意图,![]() 分别是该公园的四个入口,两条主干道
分别是该公园的四个入口,两条主干道![]() 交于点
交于点![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,请你帮助公园的管理人员解决以下问题:
,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 ![]() ;
;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() (点
(点![]() 与点
与点![]() 不重合),并计划在
不重合),并计划在![]() 与
与![]() 两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你画出该公园修建这三条绿道投入资金最小值时的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观, 从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形积的方法进行直 观推导和解释.

![]() 如图 1,是一个重要公式的几何解释,请你写出这个公式:
如图 1,是一个重要公式的几何解释,请你写出这个公式:
![]() 如图 2,在
如图 2,在![]() 中,
中,![]() ,以
,以![]() 的三边长向外作正方形的面积分别为
的三边长向外作正方形的面积分别为![]() ,试猜想
,试猜想![]() 之间存在的等量关系,直接写出结论 .
之间存在的等量关系,直接写出结论 .
![]() 如图 3,如果以
如图 3,如果以![]() 的三边长
的三边长![]() 为直径向外作半圆,那么第
为直径向外作半圆,那么第![]() 问的结论 是否成立?请说明理由.
问的结论 是否成立?请说明理由.
![]() 如图 4,在
如图 4,在![]() 中,
中,![]() ,三边分别为
,三边分别为![]() ,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com