
【题目】在平面直角坐标系内,直线![]() 与两坐标轴交于
与两坐标轴交于![]() 、
、![]() 两点,点
两点,点![]() 为坐标原点,若在该坐标平面内有以点
为坐标原点,若在该坐标平面内有以点![]() (不与点
(不与点![]() 、
、![]() 、
、![]() 重合)为顶点的直角三角形与
重合)为顶点的直角三角形与![]() 全等,且这个以点
全等,且这个以点![]() 为顶点的直角三角形与
为顶点的直角三角形与![]() 有一条公共边,则所有符合条件的
有一条公共边,则所有符合条件的![]() 点个数为( )
点个数为( )
A. 9个 B. 7个 C. 5个 D. 3个
【答案】B
【解析】
可先求得A、B两点的坐标,再分以AB为公共边,以OA为公共边和OB为公共边进行分别讨论求其坐标即可.
解:在y=![]() x+3中,令x=0则y=3,令y=0则x=-4,
x+3中,令x=0则y=3,令y=0则x=-4,
∴A为(-4,0),B为(0,3),可求得AB=5,
(Ⅰ)当以AB为公共边时,分两种情况:
(1)当PA=3,PB=4时,当P在x轴上方时,如图1,
可知∠PBA=∠BAO,
∴PB∥OA,
∴P点坐标为(-4,3),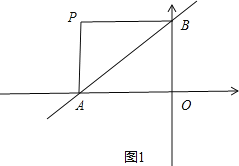
当P点在x轴下方时,如图2,设PB交AO于点C,过P作PD⊥x轴,PE⊥y轴,
∵△PAB≌△OBA,
∴PB=AO=4,PA=OB=3,
设P点坐标为(x,y),则PE=DO=-x,PD=-y,AD=4+x,BE=3-y,
在Rt△PEB中,由勾股定理可得(-x)2+(3-y)2=42,整理可得x2+y2-6y=7①,
在Rt△ADP中,由勾股定理可得(4+x)2+y2=32,整理可得x2+y2+8x=-7②,
由①、②可解得x=-![]() ,y=-
,y=-![]() ,
,
∴此时P点坐标为(-![]() ,-
,-![]() );
);
(2)当PA=4,PB=3时,
当P在x轴上时则与O点重合,
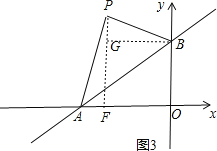
当P在x轴上方时,如图3,过P作PF⊥x轴,过B作BG⊥PF于点G,
∵△PAB≌△OBA,
∴PB=BO=3,PA=OA=4,
设P点坐标为(x,y),则PF=y,FO=BG=-x,AF=4+x,PG=y-3,
在Rt△AFP中,由勾股定理可得y2+(4+x)2=42,整理可得x2+y2+8x=0③,
在Rt△PGB中,由勾股定理可得x2+(y-3)2=32,整理可得x2+y2-6y=0④,
由③、④可解得x=-![]() ,y=
,y=![]() ,
,
∴此时P点坐标为(-![]() ,
,![]() );
);
(Ⅱ)当以AO为公共边时,分两种情况:
当P点在x上方时,与(-4,3)重合,如图4,
当P点在x下方时,当AP=BO=3时,可求得P点坐标为(-4,-3),
当PO=BO=3时,可求得P点坐标为(0,-3),
(Ⅲ)当以BO为公共边时,分两种情况:
当P点在y轴左侧时,与(-4,3)重合,如图5,
当P点在y轴右侧时,当BP=AO=4时,可求得P点坐标为(4,3),
当OP=OA=4时,可求得P点坐标为(4,0),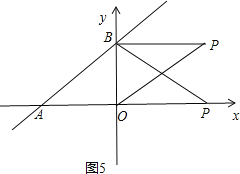
综上可知满足条件的P点共有七个,坐标分别为(-4,3)、(-![]() ,-
,-![]() )、(-
)、(-![]() ,
,![]() )、(-4,-3)、(0,-3)、(4,3)、(4,0).共7点.
)、(-4,-3)、(0,-3)、(4,3)、(4,0).共7点.
故选:B


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点,与y轴相交于点C(0,3),点B坐标是(3,0),设抛物线的顶点为点D.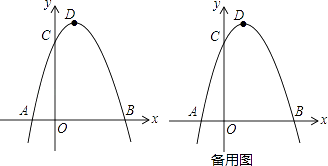
(1)求此抛物线的解析式与对称轴;
(2)作直线BC,与抛物线的对称轴交于点E,点P为直线BC上方的二次函数上一个动点(且点P与点B,C不重合),过点P作PF∥DE交直线BC于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PDEF为平行四边形?
②设△PBC的面积为S,求S与m的函数关系式.S是否存在最大值?若存在,求出最大值并求出此时P点坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
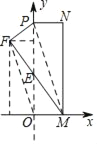
【题目】如图,在平面直角坐标系中,长方形MNPO的边OM在x轴上,边OP在y轴上,点N的坐标为(3,9),将矩形沿对角线PM翻折,N点落在F点的位置,且FM交y轴于点E,那么点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2﹣3xy+4=0,③x2 ![]() =4,④x2=0,⑤x2﹣3x﹣4=0.
=4,④x2=0,⑤x2﹣3x﹣4=0.
A.①②
B.①②④⑤
C.①③④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
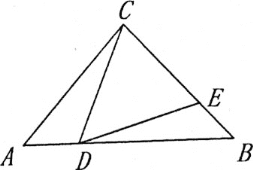
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
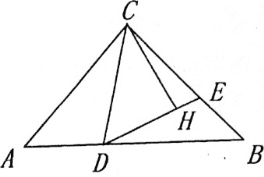
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com