练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形ABCD中，点E，F在对角线BD上，，迎接AF，CE.

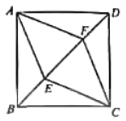
    （1）求证：；

    （2）试判断四边形AECF的形状，并说明理由.

    【答案】（1）证明见解析；（2）菱形，理由见解析.

    【解析】

    （1）根据正方形的性质可得：，，然后根据平行线的性质可得：和，从而证出，最后利用AAS即可证出；

    （2）根据全等三角形的性质可得: ,再根据平行四边形的判定可得：四边形AECF是平行四边形，然后利用SAS即可证出，从而得出，最后根据菱形的判定即可证出四边形AECF是菱形.

    解：（1）∵四边形ABCD是正方形

    ∴，

    ∴

    ∵

    ∴

    ∵，

    ∴

    ∴在与中

    ∴

    （2）四边形AECF是菱形，理由如下，

    ∵

    ∴，

    ∵

    ∴四边形AECF是平行四边形

    在与中

    ∴

    ∴

    ∴四边形AECF是菱形

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在直角中，，的垂直平分线交于点，交于点，交于点，连接、．

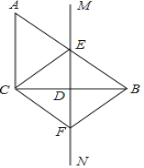
    （1）求证：；

    （2）求证：四边形是菱形．

    （3）当满足什么条件时，四边形是正方形，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．

    （1）求证：DE是⊙O的切线；

    （2）若△ABC的边长为4，求EF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

    （1）求证：△ADE≌△CBF；

    （2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据报道，从2018年8月以来“非洲猪瘟”给生猪养殖户带来了不可估量的损失，某养殖户为了预防“非洲猪瘟”的侵袭，每天对猪场进行药熏消毒，已知一瓶药物释放过程中，一个圈舍内每立方米空气中含药量y（毫克）与时间x（分钟）之间满足正比例函数关系；药物释放完后，y与x之间满足反比例函数关系，如图所示，结合图中提供的信息解答下列问题.

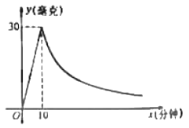
    （1）分别求当和时，y与x之间满足的函数关系式；

    （2）据测定，当空气中每立方米的含药量不低于6毫克时，消毒才有效，那么这次熏药的有效消毒时间是多少分钟？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】校园空地上有一面墙，长度为20m，用长为32m的篱笆和这面墙围成一个矩形花圃，如图所示．

    （1）能围成面积是126m2的矩形花圃吗？若能，请举例说明；若不能，请说明理由．

    （2）若篱笆再增加4m，围成的矩形花圃面积能达到170m2吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AB＝AC＝5cm，AB边上的高为3，则sinB＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有5个分别写有数字0，1，2，3，4的小球，它们除数字不同外其余全部相同.现从盒子里随机摸出一个小球（不放回），设该小球上的数字为m，再从盒子中摸出一个小球，设该小球上的数字为n，点P的坐标为，则点P落在抛物线与x轴所围成的区域内（含边界）的概率是________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关注数学文化：古希腊的几何学家海伦在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中，给出了如下公式:若一个三角形的三边长分别为a,b,c，记p=，则三角形的面积S=(海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式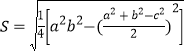：.海伦公式和秦九韶公式实质上是同一个公式，所以我们一般也称此公式为海伦-秦九韶公式.

    若△ABC的三边长分别为5，6，7，△DEF的三边长分别为，，，请选择合适的公式分别求出△ABC和△DEF的面积.

    查看答案和解析>>

    同步练习册答案