练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在直角中，，的垂直平分线交于点，交于点，交于点，连接、．

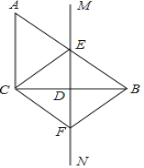
    （1）求证：；

    （2）求证：四边形是菱形．

    （3）当满足什么条件时，四边形是正方形，请说明理由．

    【答案】（1）见解析；（2）见解析；（3）当时，四边形是正方形，理由见解析

    【解析】

    （1）根据AAS证明两三角形全等；
    （2）利用全等得：BE=CF，由中垂线的性质得：CE=BE，CF=BF，则四边相等，得出四边形BECF是菱形；
    （3）根据有一个角是直角的菱形是正方形得结论．

    （1）证明：∵是的中垂线，

    ∴，

    ∵，

    ∴，，

    ∴；

    （2）证明：∵ 是的中垂线，

    ∴，，

    由（1）得，

    ∴，

    ∴，

    ∴四边形是菱形；

    （3）解：当时，四边形是正方形，理由是：

    ∵，，

    ∴，

    由（2）可得四边形是菱形，

    ∴，

    ∴，

    ∴四边形是正方形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

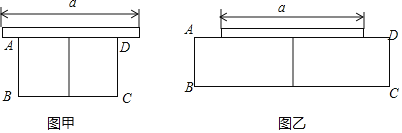
    【题目】某植物园有一块足够大的空地，其中有一堵长为a米的墙，现准备用20米的篱笆围两间矩形花圃，中间用篱笆隔开．小俊设计了如图甲和乙的两种方案：

    方案甲中AD的长不超过墙长；方案乙中AD的长大于墙长．

    （1）若a=6．

    ①按图甲的方案，要围成面积为25平方米的花圃，则AD的长是多少米？

    ②按图乙的方案，能围成的矩形花圃的最大面积是多少？

    （2）若0＜a＜6.5，哪种方案能围成面积最大的矩形花圃？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知BD：OD＝2：1，点C在射线OF上，OC＝12．点M是∠EOF内一点，MC⊥OF于点C，MC＝4．在射线CF上取一点A，连结AM并延长交射线OE于点B，作BD⊥OF于点D．

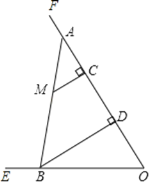
    （1）当AC的长度为多少时，△AMC和△BOD相似；

    （2）当点M恰好是线段AB中点时，试判断△AOB的形状，并说明理由；

    （3）连结BC．当S△AMC＝S△BOC时，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年沈阳国际马拉松赛事设有“马拉松”（A），“半程马拉松”（B），“10公里跑”（C），“迷你马拉松”（D）四个项目，小明和小亮参加了该赛事的志愿者服务工作，组委会将志愿者随机分配到四个项目组，被分配到每个项目组的机会是相同的．

    （1）小明被分配到“马拉松”（A）项目组的概率为　 　；

    （2）利用画树状图或列表法求小明和小亮被分配到同一个项目组进行志愿服务的概率．（项目名称可用字母表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

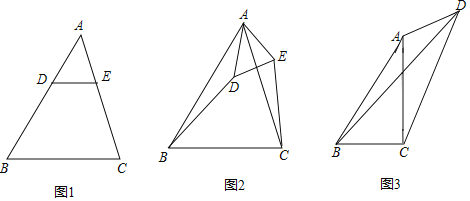
    【题目】（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝，则的值是　 　；

    （2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；

    （3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝，当CD＝6，AD＝3时，请直接写出线段BD的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

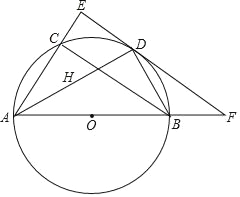
    【题目】如图，在直角三角形ABC中，∠ACB＝90°，点H是△ABC的内心，AH的延长线和三角形ABC的外接圆O相交于点D，连结DB．

    （1）求证：DH＝DB；

    （2）过点D作BC的平行线交AC、AB的延长线分别于点E、F，已知CE＝1，圆O的直径为5．

    ①求证：EF为圆O的切线；

    ②求DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

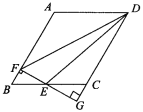
    【题目】已知：如图，□ABCD中，AB＝4，BC＝3，∠BAD＝120°，E为BC上一动点(不与B点重合)，作EF⊥AB于F，FE，DC的延长线交于点G，设BE＝x，△DEF的面积为S．

    (1)求证：△BEF∽△CEG；

    (2)求用x表示S的函数表达式，并写出x的取值范围；

    (3)当E点运动到何处时，S有最大值，最大值为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形中，，，E是边的中点，点P在边上，设，若以点D为圆心，为半径的与线段只有一个公共点，则所有满足条件的x的取值范围是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，点E，F在对角线BD上，，迎接AF，CE.

    （1）求证：；

    （2）试判断四边形AECF的形状，并说明理由.

    查看答案和解析>>

    同步练习册答案