
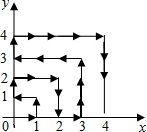
 如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),然后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个单位长度.
如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),然后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个单位长度.分析 (1)(2,2)点可以根据已知图形数出来即可.
(2)根据现有点(1,1)、(2,2)、(3,3)、(4,4)分析点的运动时间和运动方向,可以得出一般结论,设点(n,n),当n为奇数时,运动了n(n+1)分钟,方向向左;当n为偶数时,运动了n(n+1)分钟,方向向下;然后利用这个结论算出2015分钟点的坐标.
解答 解:(1)粒子所在位置与运动的时间的情况如下:
位置:(1,1)运动了2=1×2分钟,方向向左,
位置:(2,2)运动了6=2×3分钟,方向向下,
位置:(3,3)运动了12=3×4分钟,方向向左,
位置:(4,4)运动了20=4×5分钟,方向向下;
故答案为:6分钟.
(2)由(1)中总结规律发现,设点(n,n),
当n为奇数时,运动了n(n+1)分钟,方向向左;
当n为偶数时,运动了n(n+1)分钟,方向向下;
到(44,44)处,粒子运动了44×45=1980分钟,方向向下,
故到2004分钟,须由(44,44)再向下运动2015-1980=35分钟,
到达(44,9).
故答案为:(44,9).
点评 题目考查了规律型点的坐标,通过点的运动和点的坐标,考查了学生的观察能力和分析能力,对学生解决问题的能力要求较高.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:填空题
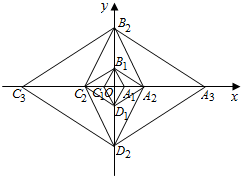 已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再A2C2以为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,则线段OA2015的长为32014.
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再A2C2以为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,则线段OA2015的长为32014.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 函数的最小值为2 | B. | 其图象与y轴的交点为(0,2) | ||
| C. | 其图象顶点坐标为(1,2) | D. | 其图象对称轴是直线x=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 出生年份 | 2022年年龄(岁) | 延迟退休时间(年) | 实际退休年龄(岁) |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4厘米 | B. | 2厘米 | C. | 小于2厘米 | D. | 不大于2厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com