
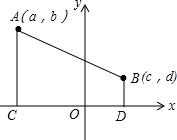 已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.分析 (1)CD的长为A、B两点的横坐标之差的绝对值;|DB-AC|为A、B两点的纵坐标之差的绝对值;
(2)写出两点间的距离公式;
(3)利用两点间的距离公式计算.
解答 解:(1)CD=|c-a|,|DB-AC|=|b-d|;
(2)AB=$\sqrt{(a-c)^{2}+(b-d)^{2}}$;
(3)AB=$\sqrt{(-2-4)^{2}+(5+4)^{2}}$=3$\sqrt{13}$.
故答案为|c-a|,|b-d|;$\sqrt{(a-c)^{2}+(b-d)^{2}}$.
点评 本题考查了两点间的距离公式:设有两点A(x1,y1),B(x2,y2),则这两点间的距离为AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.求直角坐标系内任意两点间的距离可直接套用此公式.


科目:初中数学 来源: 题型:填空题
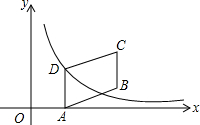 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
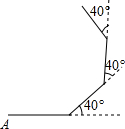 如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.
如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.| A. | 70 | B. | 80 | C. | 90 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
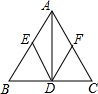 如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.
如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25的平方根是5 | B. | -22的算术平方根是2 | ||
| C. | 0.8的立方根是0.2 | D. | $\frac{5}{6}$ 是$\frac{25}{36}$的一个平方根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com