
【题目】请根据证明过程,在括号内填写相应理由,如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D,
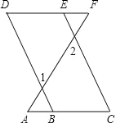
求证:∠A=∠F.
证明:因为∠1=∠2(已知)
所以BD∥CE( )所以∠C=∠ABD( )因为∠C=∠D( )
所以∠D=∠ABD( )
所以DF∥AC( )所以∠A=∠F( )
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
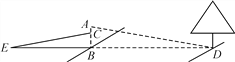
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 ;
(2)如图 1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB 为勾股边且有对角线相等的勾股四边形 OAMB 的顶点M 的坐标: ;
(3)如图 2,将△ABC 绕顶点 B 按顺时针方向旋转 60°,得到△DBE,连接 AD、DC,∠DCB=30°.求证: DC2 BC2 AC2 ,即四边形 ABCD 是勾股四边形;
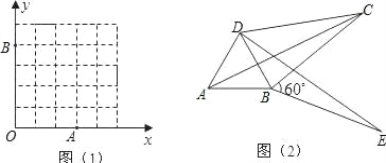
(4)若将图 2 中△ABC 绕顶点 B 按顺时针方向旋转 a 度(0°<a <90°),得到△DBE,连接 AD、DC,则当∠DCB= °时,四边形BECD 是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BAO=30°.
(1)求AB的长度;
(2)以AB为一边作等边△ABE,作OA的垂直平分线MN交AB的垂线AD于点D.求证:BD=OE;
(3)在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成如下图所示统计图:
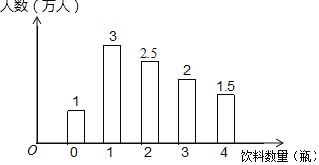
(1)在A出口的被调查游客中,购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶;
(2)已知A、B、C三个出口的游客量比为2:2:1,用上面图表的人均购买饮料数量计算:这一天景区内若有50万游客,那么这一天购买的饮料的总数是多少?
表一:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
(3)若每瓶饮料要消耗0.5元处理包装的环保费用,该日需要花费多少钱处理这些饮料瓶?由此请你对游客做一点环保宣传建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
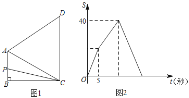
A. 10B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
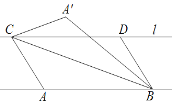
【题目】如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABDC的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BC A′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )
A. ①②③④B. ①③④C. ①②④D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com