
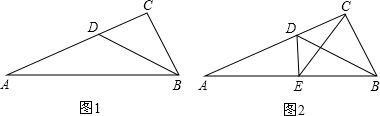
分析 (1)根据角平分线和等腰三角形的性质求得∠A=∠DBA=∠DBC,由∠A+∠DBA+∠DBC=90°,即可求得∠A=30°;
(2)根据等腰三角形三线合一的性质得出CE=BE,由∠EBC=60°,即可证得△EBC是等边三角形.
解答 (1)解:∵AD=BD,
∴∠A=∠DBA,
∵∠DBA=∠DBC,
∴∠A=∠DBA=∠DBC,
∵∠ACB=90°,
∴∠A+∠DBA+∠DBC=90°,
∴∠A=30°;
(2)证明:∵AD=BD,DE⊥AB,
∴AE=BE,
∴CE=BE,
∵∠A=30°,
∴∠EBC=60°,
∴△EBC是等边三角形.
点评 本题考查了等腰三角形的判定和性质,等边三角形的判定,直角三角形斜边中线的性质,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
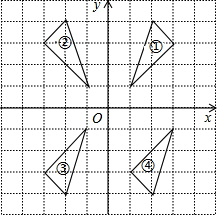 如图所示,编号为①②③④的四个三角形
如图所示,编号为①②③④的四个三角形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
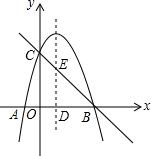 如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.
如图,抛物线y=-x2+bx+c交x轴于点B(3,0),交y轴交于点C(0,3),抛物线的对称轴交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
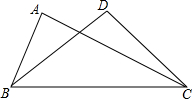 如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
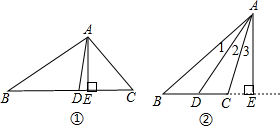 求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.
求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
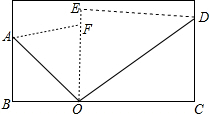 将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.
将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com