
【题目】在△ABC中,AH⊥BC于点H,点P从B点开始出发向C点运动,在运动过程中,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q (1,![]() )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=![]() ;③AC=2
;③AC=2![]() ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是________(填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是________(填写序号).
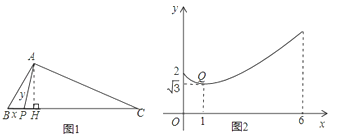
【答案】①②③④
【解析】
(1)当![]() 时,
时,![]() 的值即是
的值即是![]() 的长度;
的长度;
(2)图乙函数图象的最低点的![]() 值是
值是![]() 的值;
的值;
(3)在直角![]() 中,由勾股定理来求
中,由勾股定理来求![]() 的长度;
的长度;
(3)当点![]() 运动到点
运动到点![]() 时,此时
时,此时![]() ,
,![]() ,在
,在![]() 中,可得出
中,可得出![]() ,则判定
,则判定![]() 是等边三角形,故
是等边三角形,故![]() ,即
,即![]()
(5)分两种情况进行讨论,①![]() 为钝角,②
为钝角,②![]() 为钝角,分别确定
为钝角,分别确定![]() 的范围即可.
的范围即可.
解:(1)当![]() 时,
时,![]() 的值即是
的值即是![]() 的长度,故
的长度,故![]() ,故①正确;
,故①正确;
(2)图乙函数图象的最低点的![]() 值是
值是![]() 的值,故
的值,故![]() ,故②正确;
,故②正确;
(3)如图乙所示:![]() ,
,![]() ,则
,则![]() .
.
又![]() ,
,
![]() 直角
直角![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,故③正确;
,故③正确;
(4)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
又![]() 是等腰三角形,
是等腰三角形,
![]() 是等边三角形,
是等边三角形,
![]() ,即
,即![]() .
.
故④正确;
(5)①当![]() 为钝角时,此时可得
为钝角时,此时可得![]() ;
;
②当![]() 为钝角时,如图:过点
为钝角时,如图:过点![]() 作
作![]() ,则
,则![]() ,
,
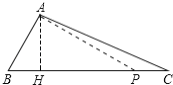
即当![]() 时,
时,![]() 为钝角.
为钝角.
综上可得![]() 或
或![]() 时
时![]() 为钝角三角形,故⑤错误.
为钝角三角形,故⑤错误.
故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某河流受暴雨影响,水位不断上涨,下面是某天此河流的水位记录:
时间(时) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
水位(米) | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
(1)上表反映的是哪两个量之间的关系?自变量和因变量各是什么?
(2)根据表格画了表示两个变量的折线统计图.
(3)哪段时间水位上升得最快?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:数x、y、z中较大的数称为max{x,y,z}.例如max{﹣3,1,﹣2}=1,函数y=max{﹣t+4,t,![]() }表示对于给定的t的值,代数式﹣t+4,t,
}表示对于给定的t的值,代数式﹣t+4,t,![]() 中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t=_________时函数y的值最小.
中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t=_________时函数y的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米.动点
厘米.动点![]() 从
从![]() 出发,以2厘米/秒的速度沿
出发,以2厘米/秒的速度沿![]() 运动,到
运动,到![]() 点停止运动;同时点
点停止运动;同时点![]() 从
从![]() 点出发,以4厘米/秒的速度沿
点出发,以4厘米/秒的速度沿![]() 运动,到
运动,到![]() 点停止运动.设
点停止运动.设![]() 点运动的时间为
点运动的时间为![]() 秒(
秒(![]() ).
).
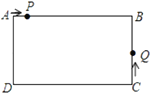
(1)点![]() 在
在![]() 上运动时,
上运动时,![]() ______,
______,![]() ______(用含
______(用含![]() 的代数式表示);点
的代数式表示);点![]() 在
在![]() 上运动时,
上运动时,![]() ______,
______,![]() ______;(用含
______;(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值,
为何值,![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点在运动路线上相距的路程为4厘米;
两点在运动路线上相距的路程为4厘米;
(4)当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知⊙O的半径为1,菱形ABCD的三个顶点A、B、D在⊙O上,且CD与⊙O相切.
(1)求证:BC与⊙O相切;
(2)求阴影部分面积.
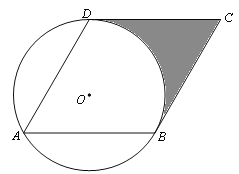
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图像如图所示。
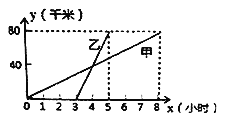
(1)请根据图像回答下列问题:甲先出发 小时后,乙才出发;在甲出发 小时后两人相遇,这时他们距A地 千米;
(2)乙的行驶速度 千米/小时;
(3)分别求出甲、乙在行驶过程中的路程(千米)与时间(小时)之间的函数关系式(不要求写出自变量的取值范围)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
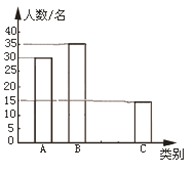
A. 900名 B. 1050名 C. 600名 D. 450名
【答案】D
【解析】分析:用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
详解:100名学生中“使用电子鞭炮”的学生有![]() 人,“使用电子鞭炮”的百分比为:
人,“使用电子鞭炮”的百分比为:![]()
全校“使用电子鞭炮”的学生有:![]() 人.
人.
故选D.
点睛:考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
【题型】单选题
【结束】
9
【题目】如图,在□ABCD中,E、F分别为BC、AD的中点,AE、CF分别交BD于点M、N,则四边形 AMCN与□ABCD的面积比为( )
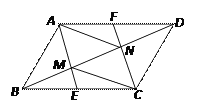
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com