
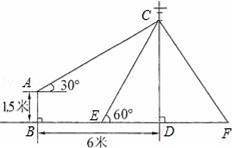
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

【考点】解直角三角形的应用-仰角俯角问题.
【专题】计算题;几何图形问题.
【分析】由题意可先过点A作AH⊥CD于H.在Rt△ACH中,可求出CH,进而CD=CH+HD=CH+AB,再在Rt△CED中,求出CE的长.
【解答】解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=
 ,
,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6×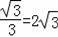
 (米),
(米),
∵DH=1.5,∴CD=2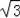
 +1.5,
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED=
 ,
,
∴CE=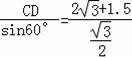
 =(4+
=(4+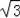
 )(米),
)(米),
答:拉线CE的长为(4+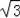
 )米.
)米.


【点评】命题立意:此题主要考查解直角三角形的应用.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:
下列事件中,属于必然事件的是( )
A.明天我市下雨
B.抛一枚硬币,正面朝下
C.购买一张福利彩票中奖了
D.掷一枚骰子,向上一面的数字一定大于零
查看答案和解析>>
科目:初中数学 来源: 题型:
一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则b2﹣4ac满足的条件是( )
A.b2﹣4ac=0 B.b2﹣4ac>0 C.b2﹣4ac<0 D.b2﹣4ac≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
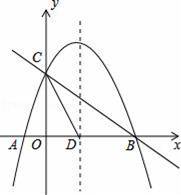
如图,抛物线y=﹣
 x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
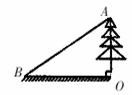
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端O点30米的B处,测得
树顶4的仰角∠ABO为α,则树OA的高度为
A.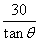 米 B.30sinα米 C.30tanα米 D.30cosα米
米 B.30sinα米 C.30tanα米 D.30cosα米
查看答案和解析>>
科目:初中数学 来源: 题型:
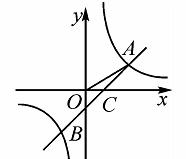
如图,反比例函数y= 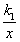 与一次函数y=k2x+b图象的交点为4(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=
与一次函数y=k2x+b图象的交点为4(m,1),B(-2,n),OA与x轴正方向的夹角为α,且tanα=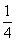 .
.
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com