

科目:初中数学 来源:不详 题型:解答题
 、
、 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
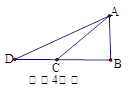
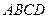 中,点
中,点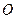 在对角线
在对角线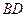 上,以
上,以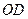 的长为半径的⊙
的长为半径的⊙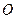 与
与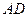 ,
,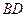 分别交于点E、点F,且∠
分别交于点E、点F,且∠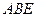 =∠
=∠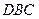 .
.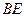 与⊙
与⊙ 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
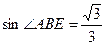 ,
,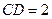 ,求⊙
,求⊙ 的半径.
的半径.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
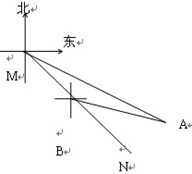
 山脚点A测得山腰上一点D的仰角为300,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为450,山腰点D的俯角为600。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
山脚点A测得山腰上一点D的仰角为300,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为450,山腰点D的俯角为600。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com