火车车厢中.如果8号车厢23号座位记为.那么9号车厢18号座位记为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

7．火车车厢中，如果8号车厢23号座位记为（8，23），那么9号车厢18号座位记为（9，18）．

分析根据有序数对（a，b），a表示车厢，b表示座位，可得答案．

解答解：∵8号车厢23号座位记为（8，23），
∴9号车厢18号座位记为：（9，18），
故答案为：（9，18）．

点评本题考查了坐标确定位置，利用有序数对（a，b），a表示车厢，b表示座位是解题关键．

练习册系列答案

考卷王单元检测评估卷系列答案

心算口算巧算一课一练系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

17．若y=（m-1）x^|m|+2，当m=-1 时，y是x的一次函数．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

18．

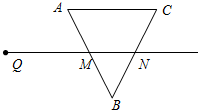如图，射线QN与边长为8的等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN．动点P从点Q出发，沿射线QN以每秒2cm的速度向右移动，以点P为圆心，2$\sqrt{3}$cm为半径的圆也随之移动．若AM=MB=4cm，QM=8cm，且经过t秒，当⊙P与△ABC的边相切时，则t可取的一切值为t=2或3≤t≤7或t=8（单位：秒）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

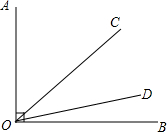如图，已知∠AOB=90°，射线OC绕点O从OA位置开始，以每秒4°的速度顺时针方向旋转；同时，射线OD绕点O从OB位置开始，以每秒1°的速度逆时针方向旋转．当OC与OA成180°时，OC与OD同时停止旋转．
（1）当OC旋转10秒时，∠COD=40°．
（2）当OC与OD的夹角是30°时，求旋转的时间．
（3）当OB平分∠COD时，求旋转的时间．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．（1）已知：如图1，点O为直线AB上任意一点，射线OC为任意一条射线．OD、OE分别平分∠AOC和∠BOC，则∠DOE=90°；
（2）已知：如图2，点O为直线AB上任意一点，射线OC为任意一条射线，其中∠COD=$\frac{1}{3}$∠AOC，∠COE=$\frac{1}{3}$∠BOC，求∠DOE得度数；
（3）如图3，点O为直线AB上任意一点，OD是∠AOC的平分线，OE在∠BOC内，∠COE=$\frac{1}{3}$∠BOC，∠DOE=72°，求∠BOE的度数．