
已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.


【考点】矩形的性质;全等三角形的判定与性质;线段垂直平分线的性质;勾股定理;平行四边形的判定与性质;菱形的判定与性质.
【分析】(1)先证明四边形AFCE为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;根据勾股定理即可求得AF的长;
(2)①分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
②分三种情况讨论可知a与b满足的数量关系式.
【解答】解:(1)①∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,
∴OA=OC,
∴△AOE≌△COF,
∴OE=OF,
∴四边形AFCE为平行四边形,
又∵EF⊥AC,
∴四边形AFCE为菱形,
②设菱形的边长AF=CF=xcm,则BF=(8﹣x)cm,
在Rt△ABF中,AB=4cm,
由勾股定理得42+(8﹣x)2=x2,
解得x=5,
∴AF=5cm.
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=CD+AD﹣4t=12﹣4t,即QA=12﹣4t,
∴5t=12﹣4t,
解得
 ,
,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,
 秒.
秒.
②由题意得,四边形APCQ是平行四边形时,点P、Q在互相平行的对应边上.
分三种情况:
i)如图1,当P点在AF上、Q点在CE上时,AP=CQ,即a=12﹣b,得a+b=12;
ii)如图2,当P点在BF上、Q点在DE上时,AQ=CP,即12﹣b=a,得a+b=12;
iii)如图3,当P点在AB上、Q点在CD上时,AP=CQ,即12﹣a=b,得a+b=12.
综上所述,a与b满足的数量关系式是a+b=12(ab≠0).






 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
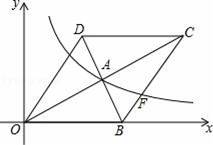
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=
 (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点A的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点A的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
小明手里有6张完全一样的卡片,其中4张正面画上记号“A”,另外2张卡片被画上记号“B”,先将其背面朝上洗匀,让小东从中随机抽取2张卡片,则他抽出的两张均有“A”记号的卡片的概率等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )


A.圆 B.椭圆
C.一般的平行四边形 D.矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图.
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形统计图中m的值和“E”组对应的圆心角度数;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.


查看答案和解析>>
科目:初中数学 来源: 题型:
.下列命题中,真命题是( )
A.四边相等的四边形是正方形
B.对角线相等的菱形是正方形
C.正方形的两条对角线相等,但不互相垂直平分
D.矩形、菱形、正方形都具有“对角线相等”的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
某学习小组设计了一个摸球试验,在袋中装有黑,白两种颜色的球,这些球的形状大小质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋中摸出一个球,记下颜色,再把它放回,不断重复.下表是由试验得到的一组统计数据:
| 摸球的次数 | 100 | 200 | 300 | 400 | 500 | 600 |
| 摸到白球的次数 | 58 | 118 | 189 | 237 | 302 | 359 |
| 摸到白球的频率 | 0.58 | 0.59 | 0.63 | 0.593 | 0.604 | 0.598 |
从这个袋中随机摸出一个球,是白球的概率约为 .(结果精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com