
����Ŀ����֪��ABC�ǵ���ֱ�������Σ���BAC=90�㣬CD= ![]() BC��DE��CE��DE=CE������AE����M��AE���е㣮
BC��DE��CE��DE=CE������AE����M��AE���е㣮 
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij���
��2����ͼ2������D�ڡ�ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤��MN��AE��
��3����ͼ3����ͼ2�еġ�CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30�㣬����BD����N��BD�е㣬����MN��̽�� ![]() ��ֵ��ֱ��д�������
��ֵ��ֱ��д�������
���𰸡�
��1��
�⣺��ͼ1�У�
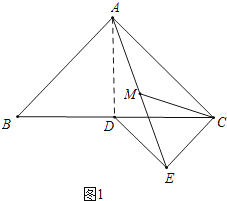
����AD��
��AB=AC=4����BAC=90�㣬
���B=��ACD=45�㣬BC= ![]() =4
=4 ![]() ��
��
��DC= ![]() BC=2
BC=2 ![]() ��
��
��ED=EC����DEC=90�㣬
��DE=EC=2����DCE=��EDC=45�㣬
���ACE=90�㣬
��RT��ACE��AE= ![]() =
= ![]() =2
=2 ![]() ��
��
��AM=ME��
��CM= ![]() AE=
AE= ![]()
��2��
֤������ͼ2�У�

�ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F��
�ڡ�AMG�͡�EMD�У�
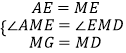 ��
��
���AMG�ա�EMD��
��AG=DE=EC��
��MAG=��MED��
��EF��AG��
���BAG=��BFE=180�㩁��FBC����90�㩁��ECB��=45��+��BCE=��ACE��
�ڡ�ABG�͡�CAE�У�
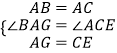 ��
��
���ABG�ա�CAE��
���ABG=��CAE��
�ߡ�CAE+��BAE=90�㣬
���ABG+��BAE=90�㣬
���AOB=90�㣬
��BG��AE��
��DN=NB��DM=MG��
��MN��BG��
��MN��AE
��3��
�⣺��ͼ3�У�
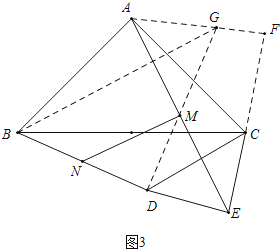
�ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F��
�ߡ�AMG�ա�EMD��
��AG=DE=EC����GAM=��DEM��
��AG��DE��
���F=��DEC=90�㣬
�ߡ�FAC+��ACF=90�㣬��BCD+��ACF=90�㣬��BCD=30�㣬
���BAG=��ACE=120�㣬
�ڡ�ABG�͡�CAE�У�
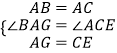 ��
��
���ABG�ա�CAE��
��BG=AE��
��BN=ND��DM=MG��
��BG=AE=2MN��
���FAC=��BCD=30�㣬��BC=2a����CD=a��DE=EC= ![]() a��AC=
a��AC= ![]() a��CF=
a��CF= ![]() a��AF=
a��AF= ![]() a��EF=
a��EF= ![]() a��
a��
��AE= ![]() =
= ![]() a��
a��
��MN= ![]() a��
a��
�� ![]() =
= ![]() =
= ![]()
����������1����֤����ACE��ֱ�������Σ�����CM= ![]() AE�����AE���ɽ�����⣮��2����ͼ2�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F����֤����AMG�ա�EMD���Ƴ�EF��AG����֤����ABG�ա�CAE���á�ABG=��CAE���ɴ˼��ɽ�����⣮��3����ͼ3�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F����֤����ABG�ա�CAE���õ�BG=AE����BC=2a����RT��AEF�����AE��������λ�߶���MN=
AE�����AE���ɽ�����⣮��2����ͼ2�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F����֤����AMG�ա�EMD���Ƴ�EF��AG����֤����ABG�ա�CAE���á�ABG=��CAE���ɴ˼��ɽ�����⣮��3����ͼ3�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F����֤����ABG�ա�CAE���õ�BG=AE����BC=2a����RT��AEF�����AE��������λ�߶���MN= ![]() BG=
BG= ![]() AE���ɴ˼��ɽ�����⣮���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������Ӹ����ߣ�����ȫ�������Σ�ѧ�����Ӹ����ߵķ����������п�ѹ���⣮
AE���ɴ˼��ɽ�����⣮���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������Ӹ����ߣ�����ȫ�������Σ�ѧ�����Ӹ����ߵķ����������п�ѹ���⣮
�����㾫�������չ��ɶ����ĸ�������������ε��ж��������ǽ����ĸ�������Ҫ֪��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��BD�ǡ�O��ֱ����AE��CD�ڵ�E��DAƽ�֡�BDE�� 
��1����֤��AE�ǡ�O�����ߣ�
��2�����AB=4��AE=2�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ֳ���ƻ�����ס����������繲700β����������ÿβ3Ԫ����������ÿβ5Ԫ��������ϱ������ס�����������ijɻ��ʷֱ�Ϊ85%��90%
��1�����������������繲��ȥ2500Ԫ����ס�������������������β��
��2����Ҫʹ����������ܳɻ��ʲ�����88%�������������������β��
��3����������繺��mβ����������ķ���ΪwԪ���г�w��x֮��ĺ�����ϵʽ������һ�κ��������ʽ�����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����һ��ͼ�Σ�����ͼ���й���2���ǣ�ͼ���й���6���ǣ�ͼ���й���11���ǣ�ͼ���й���17���ǣ��������˹��ɣ�ͼ�������ǵĿ����ǣ�������
A.43
B.45
C.51
D.53
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�齨���鷨�����֡��������赸���ݽ�������ţ�ȫУ1600��ѧ��ÿ�˶��μ���ֻ�μ�������һ�����ŵĻ��У��ί����1600��ѧ�������ѡȡ����ѧ�������˲μӻ����ĵ��飬�����������Ƴ�����ͼ��������ͳ��ͼ�������ͳ��ͼ����������⣺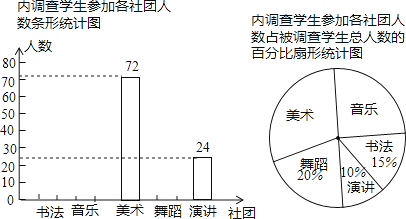
�μӱ��ε�������ѧ�������ݵ������ݷ�����ȫУԼ����ѧ���μ����������ţ����㲹ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��DEƽ�֡�ADO��AC�ڵ�E���ѡ�ADE��AD���ۣ��õ���ADE�䣬��F��DE���е㣬����AF��BF��E��F����AE= ![]() �����ı���ABFE�������� ��
�����ı���ABFE�������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+
x2+ ![]() x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��E��
x+3��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��E��
��1���жϡ�ABC����״����˵�����ɣ�
��2������B��C�����ֱ�߽������ߵĶԳ����ڵ�D����PΪֱ��BC�Ϸ��������ϵ�һ���㣬����PCD��������ʱ��Q�ӵ�P�����������ʵ���·���˶��������ߵĶԳ����ϵ�M�������ش�ֱ�������߶Գ���ķ����˶���y���ϵĵ�N����������ʵ���·���˶�����A��ֹͣ������Q���˶�·�����ʱ�����N�����꼰��Q���������·���ij���
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���E������AE���ƶ�����Eƽ�ƺ�Ķ�Ӧ��Ϊ��E�䣬��A�Ķ�Ӧ��Ϊ��A�䣬����AOC�Ƶ�O˳ʱ����ת����A1OC1��λ�ã���A��C�Ķ�Ӧ��ֱ�Ϊ��A1 �� C1 �� �ҵ�A1ǡ������AC�ϣ�����C1A�䣬C1E�䣬��A��C1E���Ƿ���Ϊ���������Σ����ܣ���������з��������ĵ�E������ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���EΪBC��һ�㣬FΪDE���е㣬�ҡ�BFC=90�㣮
��1����EΪBC�е�ʱ����֤����BCF�ա�DEC��
��2����BE=2ECʱ���� ![]() ��ֵ��
��ֵ��
��3����CE=1��BE=n������C����DE�ĶԳƵ�C�䣬����FC�䣬AF������C�䵽AF�ľ����� ![]() ����n��ֵ��
����n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������У�ÿ��С�����εı߳����ǵ�λ1����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��
��1����������ABC����ƽ��2����λ�õ���A1B1C1��
��2����������ABC�Ƶ�O˳ʱ�뷽����ת90��õ��ġ�A2B2C2��
��3�����A1B1C1���A2B2C2�غϲ��ֵ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com