
分析 (1)根据一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低2元,得出260-2(x-10)=224求出即可;
(2)根据利润关系式,列出一元二次方程,求出件数;
(3)由于此次购买数量大于10件,根据已知,设利润为y,根据条件列出二次函数关系式,利用对称轴性质求出a的取值范围.
解答 解:(1)设商家一次购买该产品x件时,销售单价恰好为224元.
260-2(x-10)=224,
解得:x=28;
答:顾客一次购买A产品28件时,销售单价恰好为224元.
(2)设本次交易中小张购买产品的件数是x,
∵792>(260-200)×10,
∴x>10,
根据题意得:[260-2(x-10)-200]x=792,
解得:x1=22,x2=18,
∴本次交易中小张购买产品的件数是22件或18件;
(3)设公司获利为y,则y=[260-2(x-10)-5-a-200]x-100,
即y=-2x2+(75-a)x-100,对称轴x=-$\frac{75-a}{-4}$=$\frac{75-a}{4}$,
∵顾客一次购买的数量越多,公司在该次交易中所获得的利润越大,
$\frac{75-a}{4}$≥17
解得:a≤7,
∴a的取值范围为:0≤a≤7.
点评 此题主要考查了二次函数的应用以及二次函数最值问题,根据已知建立函数关系式,借助二次函数解决实际问题是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
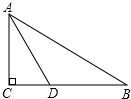 如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.
如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com