Question

已知某工厂计划用库存的302m3木料为某学校生产500套桌椅，供该校1250名学生使用，该厂生产的桌椅分为A，B两种型号，有关数据如下：

桌椅型号	一套桌椅所坐学生人数（单位：人）	生产一套桌椅所需木材（单位：m3）	一套桌椅的生产成本（单位：元）	一套桌椅的运费（单位：元）
A	2	0.5	100	2
B	3	0.7	120	4

 

设生产A型桌椅x（套），生产全部桌椅并运往该校的总费用（总费用=生产成本+运费）为y元．

（1）求y与x之间的关系式，并指出x的取值范围；

（2）当总费用y最小时，求相应的x值及此时y的值．

 

Answer 1

（1）y=﹣22x+62000，（240≤x≤250）；

（2）生产甲型桌椅250套，乙型桌椅250套，最少总费用56500元．

【解析】

试题分析：（1）利用总费用y=生产桌椅的费用+运费列出函数关系，根据需用的木料不大于302列出一个不等式，两种桌椅的椅子数不小于学生数1250列出一个不等式，两个不等式组成不等式组，得出x的取值范围；

（2）利用一次函数的增减性即可确定费用最少的方案以及费用．

试题解析：（1）设生产甲型桌椅x套，则生产乙型桌椅的套数（500﹣x）套，

根据题意得，，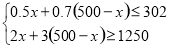

解这个不等式组得，240≤x≤250；

总费用y=（100+2）x+（120+4）（500﹣x）=102x+62000﹣124x=﹣22x+62000，

即y=﹣22x+62000，（240≤x≤250）；

（2）∵y=﹣22x+62000，﹣22＜0，

∴y随x的增大而减小，

∴当x=250时，总费用y取得最小值，

此时，生产甲型桌椅250套，乙型桌椅250套，最少总费用y=﹣22×250+62000=56500元．

考点：1、一元一次不等式组的应用；2、一次函数的应用