
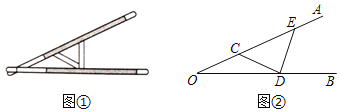
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有糟的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠AOB是______°.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD=CA,且![]() .
.

(1)求证:![]() 是⊙O的切线.
是⊙O的切线.
(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
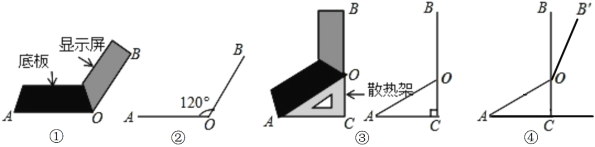
【题目】小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线![]() 与底板的边缘线
与底板的边缘线![]() 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点
所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线![]() 与水平线的夹角仍保持120°,求点
与水平线的夹角仍保持120°,求点![]() 到
到![]() 的距离.(结果保留根号)
的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
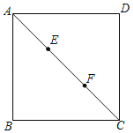
【题目】如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=9,点P在正方形的边上,则满足PE+PF=8的点P的个数是( )
A.8B.6C.4D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
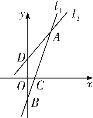
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的解析式为:
的解析式为:![]() ,若将直线
,若将直线![]() 绕
绕![]() 点旋转.如图所示,当直线
点旋转.如图所示,当直线![]() 旋转到
旋转到![]() 位置时,
位置时,![]() 且
且![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ;当直线
;当直线![]() 旋转到
旋转到![]() 位置时,
位置时,![]() 且
且![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)直接写出![]() 、
、![]() 、
、![]() 三点的坐标,连接
三点的坐标,连接![]() ,计算
,计算![]() 的面积;
的面积;
(3)已知坐标平面内一点![]() ,其坐标满足条件
,其坐标满足条件![]() ,当点
,当点![]() 与点
与点![]() 距离最小时,直接写出
距离最小时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.

(1)l经过点B,求它的解析式,并写出此时l的对称轴及顶点坐标:
(2)设点C的纵坐标为yc,求yc的最大值,此时l上有两点(x1,y1),(x2,y2),其中x1>x2≥0,比较y1与y1的大小;
(3)当线段OA被l只分为两部分,且这两部分的比是1:4时,求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
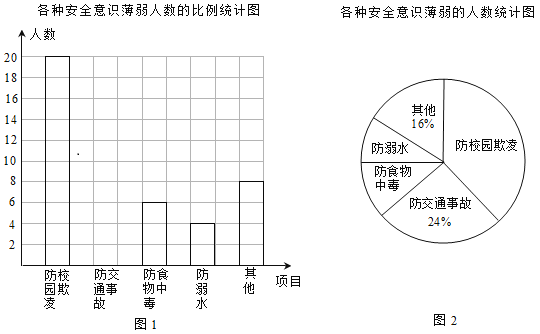
【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题:
(1)本次调查的人数为___________,其中防校园欺凌意识薄弱的人数占_________%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com