
【题目】如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD=CA,且![]() .
.

(1)求证:![]() 是⊙O的切线.
是⊙O的切线.
(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接OC,∠CAD=∠D=30°,由OC=OA,进而得到∠OCA=∠CAD=30°,由三角形外角定理得到∠COD=∠A+∠OCA=60°,在△OCD中由内角和定理可知∠OCD=90°即可证明;
(2)证明AC是∠EAG的角平分线,CB是∠FCG的角平分线,得到CE=CG,CF=CG,再证明△AEC∽△CFB,对应线段成比例即可求解.
解:(1)连接OC,如下图所示:
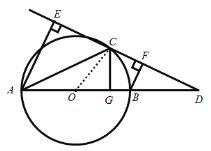
∵CA=CD,且∠D=30°,
∴ ∠CAD=∠D=30°,
∵ OA=OC,
∴ ∠CAD=∠ACO=30°,
∴∠COD=∠CAD+∠ACO=30°+30°=60°,
∴∠OCD=180°-∠D-∠COD=180°-30°-60°=90°,
∴ OC⊥CD,
∴ CD是⊙O的切线.
(2)连接BC,如下图所示:
∵∠COB=60°,且OC=OB,
∴△OCB为等边三角形,∠CBG=60°,
又CG⊥AD,∴∠CGB=90°,
∴∠GCB=∠CGB-∠CBG=30°,
又∠GCD=60°,
∴CB是∠GCD的角平分线,且BF⊥CD,BG⊥CG,
∴BF=BG,
又BC=BC,
∴△BCG≌△BCF,
∴CF=CG.
∵∠D=30°,AE⊥ED,∠E=90°,
∴∠EAD=60°,
又∠CAD=30°,
∴AC是∠EAG的角平分线,且CE⊥AE,CG⊥AB
∴CE=CG,
∵∠E=∠BFC=90°,∠EAC=30°=∠BCF,
∴△AEC∽△CFB,
∴![]() ,即
,即![]() ,
,
又![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
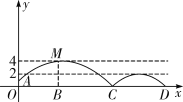
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)足球第一次落地点C距守门员多少米?(取![]() )
)
(3)运动员乙要抢到足球第二个落点D,他应再向前跑多少米?(取![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
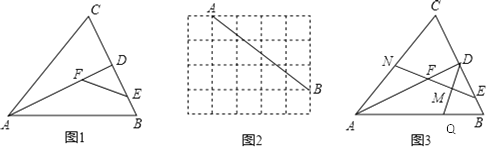
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上.
(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=6,求邻余线AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+2mx+2n,交x轴于A,B两点(A在B的左侧)
(1)当m=3时,n=4时, ①求A、B两点坐标;②将抛物线向右平移k个单位后交x轴于M、N(M在N的左侧),若B、M三等分AN,直接写出k的值;
(2)当m=1时,若线段AB上有且只有5个点的横坐标为整数,求n的取值范围;
(3)记A(x1,0)、B(x2,0),当m、n都是奇数时,x1、x2能否是有理数?若能,请举例验证,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图:
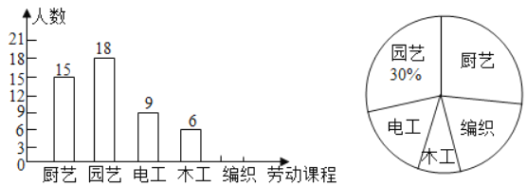
(1)本次随机调查的学生人数为 人;
(2)补全条形统计图;
(3)若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;
(4)七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
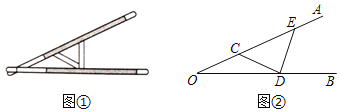
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有糟的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠AOB是______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com