
【题目】小华同学将笔记本电脑水平放置在桌子上,当是示屏的边缘线![]() 与底板的边缘线
与底板的边缘线![]() 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点
所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() ,
,![]() ,
,![]() .
.
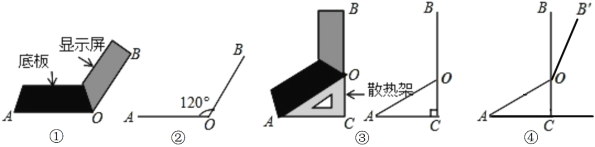
(1)求![]() 的长;
的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线![]() 与水平线的夹角仍保持120°,求点
与水平线的夹角仍保持120°,求点![]() 到
到![]() 的距离.(结果保留根号)
的距离.(结果保留根号)
【答案】(1)12cm;(2)点![]() 到
到![]() 的距离为(12+12
的距离为(12+12![]() )cm.
)cm.
【解析】
(1)在Rt△AOC中,由30度角所对的直角边长度是斜边的一半求解即可;
(2)过点O作OM∥AC,过点B′作B′E⊥AC交AC的延长线于点E,交OM于点D,B′E即为点![]() 到
到![]() 的距离,根据题意求出∠OB′D=30°,四边形OCED为矩形,根据B′E=B′D+DE求解即可.
的距离,根据题意求出∠OB′D=30°,四边形OCED为矩形,根据B′E=B′D+DE求解即可.
解:(1)∵![]() ,
,![]() ,
,![]()
∴![]() .
.
即OC的长度为12cm.
(2)如图,过点O作OM∥AC,过点B′作B′E⊥AC交AC的延长线于点E,交OM于点D,B′E即为点![]() 到
到![]() 的距离,
的距离,
∵OM∥AC,B′E⊥AC,
∴B′E⊥OD,
∵MN∥AC,
∴∠NOA=∠OAC=30°,
∵∠AOB=120°,
∴∠NOB=90°,
∵∠NOB′=120°,
∴∠BOB′=120°-90°=30°,
∵BC⊥AC,B′E⊥AE,MN∥AE,
∴BC∥B′E,四边形OCED为矩形,
∴∠OB′D=∠BOB′=30°,DE=OC=12cm,
在Rt△B′OD中,∵∠OB′D=30°,B′O=BO=24cm,
∴![]()
B′D= ![]() ,
,
B′E=B′D+DE= ![]() ,
,
答:点![]() 到
到![]() 的距离为
的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
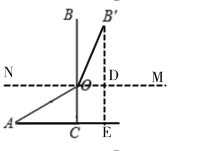
(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形.
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上.
(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=6,求邻余线AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如下两幅不完整的统计图:
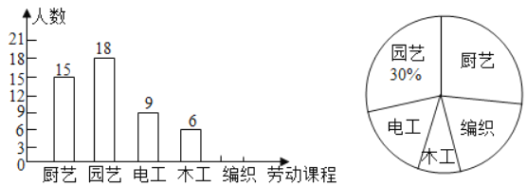
(1)本次随机调查的学生人数为 人;
(2)补全条形统计图;
(3)若该校七年级共有800名学生,请估计该校七年级学生选择“厨艺”劳动课程的人数;
(4)七(1)班计划在“园艺、电工、木工、编织”四大类劳动课程中任选两类参加学校期末展示活动,请用列表或画树状图的方法,求恰好选中“园艺、编织”这两类劳动课程的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有糟的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠AOB是______°.
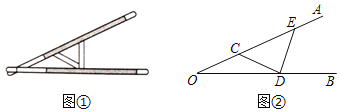
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 是线段
是线段![]() 上一动点(与点
上一动点(与点![]() 、
、![]() 不重合),连结
不重合),连结![]() ,延长
,延长![]() 至点
至点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)用等式表示![]() 与
与![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com