
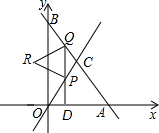
 ��֪��ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$��x�ᣬy���ཻ��A��B���㣬ֱ��y=$\sqrt{3}$x��AB�ཻ��C�㣬��D�ӵ�O��������ÿ��1����λ���ٶ���x�������˶�����A������D��x��Ĵ��ߣ��ֱ�ֱ��y=$\sqrt{3}$x��ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$��P��Q���㣨P�㲻��C���غϣ�����PQΪ������������PQR�����D���˶�ʱ��Ϊt���룩
��֪��ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$��x�ᣬy���ཻ��A��B���㣬ֱ��y=$\sqrt{3}$x��AB�ཻ��C�㣬��D�ӵ�O��������ÿ��1����λ���ٶ���x�������˶�����A������D��x��Ĵ��ߣ��ֱ�ֱ��y=$\sqrt{3}$x��ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$��P��Q���㣨P�㲻��C���غϣ�����PQΪ������������PQR�����D���˶�ʱ��Ϊt���룩���� ��1����y=0������A��ĺ����ꣻ��x=0������B��ĺ����ꣻֱ��y=$\sqrt{3}$x��ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$��������C�����ꣻ
��2������ֻ�迼�ǵ�M��2��3$\sqrt{3}$�������ڡ�PQR��ij���ϣ����t��ȡֵ���ɣ�
��� �⣺��1����y=0����0=-$\sqrt{3}$x+6$\sqrt{3}$��
��ã�x=6��
��A��������6��0����
��x=0����y=-$\sqrt{3}$��0+6$\sqrt{3}$��
��ã�y=6$\sqrt{3}$��
��B�����������0��6$\sqrt{3}$����
��ֱ��y=$\sqrt{3}$x��AB�ཻ��C�㣬
��$\left\{\begin{array}{l}{y=-\sqrt{3}x+6\sqrt{3}}\\{y=\sqrt{3}x}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=3}\\{y=3\sqrt{3}}\end{array}\right.$��
���C��������3��3$\sqrt{3}$����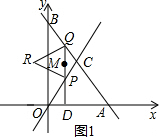
��2����P��ֱ��y=$\sqrt{3}$x�ϣ�
��tan��POD=$\frac{PD}{OD}=\sqrt{3}$��
���POD=60�㣬��OPD=30��
��OD=t��
��PD=$\sqrt{3}$t��
��Q��ֱ��y=-$\sqrt{3}$x+6$\sqrt{3}$�ϣ�
��DQ=-$\sqrt{3}t+6\sqrt{3}$��
��M��QP�ϣ���ͼ1��
��PD��x�ᣬOD=t��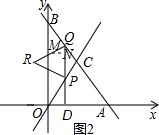
��M��2��3$\sqrt{3}$����
��t=2��
��M��RQ�ϣ���ͼ2����M��MN��PQ��N��
�ߡ�PQR�ǵȱ������Σ�
���MQN=60�㣬
���MQN�ס�PDO��
��$\frac{MN}{PD}=\frac{QN}{OD}$��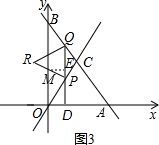
��$\frac{t-2}{\sqrt{3}t}=\frac{-\sqrt{3}t+6\sqrt{3}-3\sqrt{3}}{t}$��
��t=$\frac{11}{4}$��
��M��RP��ʱ����ͼ3����M��ME��PQ��E��
ͬ����MPE�ס�POD��
��$\frac{ME}{PD}=\frac{PE}{OD}$��
��$\frac{2-t}{\sqrt{3}t}=\frac{3\sqrt{3}-\sqrt{3}t}{t}$��
��t=$\frac{7}{2}$��
������������M��2��3$\sqrt{3}$�������ڡ�PQR��ij���ϣ�t��ֵΪ2��$\frac{11}{4}$��$\frac{7}{2}$��
���� ���⿼���˽��Ԫһ�η������������꣬�������Ǻ���ֵ��ǵĶ������ȱ������ε����ʣ����������ε��ж������ʣ���ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
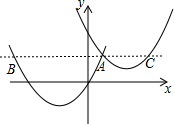 ��ͼ�������κ���y2=��x-$\frac{7}{4}$��2-2��ͼ����ƽ��m����λ������κ���y1=��x+2��2-4��ͼ���ཻ�ڵ�A����A��x���ƽ���߷ֱ�y1��y2�ڵ�B��C����AC=$\frac{1}{2}$BAʱ��m��ֵ��$\frac{43}{16}$��
��ͼ�������κ���y2=��x-$\frac{7}{4}$��2-2��ͼ����ƽ��m����λ������κ���y1=��x+2��2-4��ͼ���ཻ�ڵ�A����A��x���ƽ���߷ֱ�y1��y2�ڵ�B��C����AC=$\frac{1}{2}$BAʱ��m��ֵ��$\frac{43}{16}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
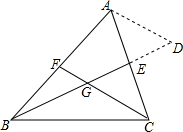 ��ͼ����ABC������BE��CF�ཻ�ڵ�G����ͼ�����Ӹ����ߵķ������ӳ�BE��D��GD=BG������AD��֤����BG=2GE��CG=2GF��
��ͼ����ABC������BE��CF�ཻ�ڵ�G����ͼ�����Ӹ����ߵķ������ӳ�BE��D��GD=BG������AD��֤����BG=2GE��CG=2GF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
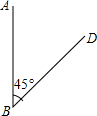 ��ͼ��ʾ��ij���ھ�A�����Ϸ���100�����B���ر�ƫ��45��ķ����У���֪A����Χ40����ķ�Χ���а������ʸô��ش˷����Ƿ���д�����Σ�գ�
��ͼ��ʾ��ij���ھ�A�����Ϸ���100�����B���ر�ƫ��45��ķ����У���֪A����Χ40����ķ�Χ���а������ʸô��ش˷����Ƿ���д�����Σ�գ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com