
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标 .

【答案】(1)![]() ;(2) (0,4)或(0,2+
;(2) (0,4)或(0,2+![]() )或(0,2﹣
)或(0,2﹣![]() )或(0,
)或(0,![]() ).
).
【解析】(1)直接利用两点间的距离公式即可得出结论;
(2)分三种情况讨论,利用等腰三角形的性质建立方程求解即可.
(1)∵A(2,3),B(0,2),∴AB=![]() =
=![]() .
.
故答案为:![]() ;
;
(2)设点C(0,m).
∵A(2,3),B(0,2),∴BC=|m﹣2|,AC=![]() ,由(1)知,AB=
,由(1)知,AB=![]() .
.
∵△ABC是等腰三角形,∴分三种情况讨论:
①当AB=AC时,∴![]() =
=![]() ,∴m=2(舍)或m=4,∴C(0,4);
,∴m=2(舍)或m=4,∴C(0,4);
②当AB=BC时,|m﹣2|=![]() ,∴m=2
,∴m=2![]() ,∴C(0,2+
,∴C(0,2+![]() )或(0,2﹣
)或(0,2﹣![]() );
);
③当AC=BC时,|m﹣2|=![]() ,∴m=
,∴m=![]() ,∴C(0,
,∴C(0,![]() ).
).
即:C(0,4)或(0,2+![]() )或(0,2﹣
)或(0,2﹣![]() )或(0,
)或(0,![]() ).
).
故答案为:(0,4)或(0,2+![]() )或(0,2﹣
)或(0,2﹣![]() )或(0,
)或(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.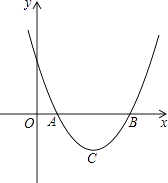
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距900m,甲乙两人同时从A地出发匀速前往B地,甲到达B地时乙距B地300m.甲到达B地后立刻以原速返回A地,返回途中与乙相遇,相遇后乙也立刻以原速向A地返回.甲、乙离A地的距离y1、y2与他们出发的时间t的函数关系如图所示.
(1)a= ; b= ;
(2)写出点C表示的实际意义 及点C的坐标
(3)甲出发多长时间,两人相距175m?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-8)+10-2+(-1); (2)12-7×(-4)+8÷(-2);
(3)(![]() )÷(-
)÷(-![]() ); (4)-14-(1+0.5)×
); (4)-14-(1+0.5)×![]() ÷(-4)2.
÷(-4)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1,图2所提供的信息,解答下列问题: 
(1)2007年海南省城镇居民人均可支配收入为元,比2006年增长%;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年(填“增加”或“减少”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时. 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,

请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
例:当a>0时,如a=6则|a|=|6|=6,故此时a的绝对值是它本身;
当a=0时,|a|=0,故此时a的绝对值是零;
当a<0时,如a=﹣6则|a|=|﹣6|=﹣(﹣6),故此时a的绝对值是它的相反数.
∴综合起来一个数的绝对值要分三种情况,即
|a|=  ,问:
,问:
(1)这种分析方法涌透了数学思想.
(2)请仿照例中的分类讨论的方法,分析二次根式 ![]() 的各种展开的情况.
的各种展开的情况.
(3)猜想 ![]() 与|a|的大小关系.
与|a|的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题:化简 ![]() (﹣3≤x≤5).
(﹣3≤x≤5).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com