
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.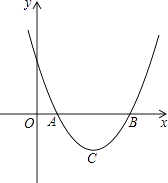
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
【答案】
(1)
解:当△ABC为等腰直角三角形时,过C作CD⊥AB于D,则AB=2CD;
∵抛物线与x轴有两个交点,
∴△>0,
∴|b2﹣4ac|=b2﹣4ac,
∵AB= ![]() ,
,
又∵CD= ![]() (a≠0),
(a≠0),
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴b2﹣4ac= ![]() ,
,
∵b2﹣4ac≠0,
∴b2﹣4ac=4
(2)
解:如图,当△ABC为等边三角形时,
由(1)可知CE= ![]() AE=
AE= ![]() AB,
AB,
∴ ![]() =
= ![]() ×
× ![]() ,
,
∵b2﹣4ac>0,
∴ ![]() =
= ![]() ,
,
∴b2﹣4ac=12.
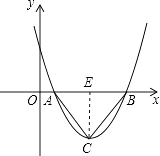
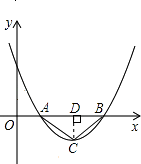
【解析】(1)由于抛物线与x轴有两个不同的交点,所以b2﹣4ac>0;可求得线段AB的表达式,利用公式法可得到顶点C的纵坐标,进而求得斜边AB上的高(设为CD),若△ABC为等腰直角三角形,那么AB=2CD,可根据这个等量关系求出b2﹣4ac的值;(2)当△ABC为等边三角形时,解直角△ACE,得CE= ![]() AE=
AE= ![]() AB,据此列出方程,解方程求出b2﹣4ac的值.
AB,据此列出方程,解方程求出b2﹣4ac的值.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
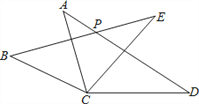
【题目】如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为 __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,AD=a,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:DF=FE;
(2)若AC=2CF,∠ADC=60°,AC⊥DC,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是__________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣15.5 | ﹣5 | ﹣3.5 | ﹣2 | ﹣3.5 | … |
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射靶![]() 次,将射击结果作统计分析如下:
次,将射击结果作统计分析如下:
命中环数 |
|
|
|
|
|
| 平均数 | 众数 | 方差 | |
甲命中环数的次数 |
|
|
|
|
|
|
|
|
| |
乙命中环数的次数 |
|
|
|
|
|
| ________ | ________ | ________ |
![]() 请你完成上表中乙进行射击练习的相关数据;
请你完成上表中乙进行射击练习的相关数据;
![]() 根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.
根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣9.8)﹣(+6);
(2)4.7﹣(﹣8.9)﹣7.5+(﹣6);
(3)1﹣3+5﹣7+9﹣11+…+97﹣99
(4)1.75+(﹣6![]() )+3
)+3![]() +(﹣1
+(﹣1![]() )+(+2
)+(+2![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D在BC边上,将△ABD绕点A按逆时针方向旋转得到△ACE,连接DE,则图中与∠BAD相等的角,除∠CAE外,还有角 . (用三个字母表示该角) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(2,3)和(0,2).
(1)AB的长为 ;
(2)点C在y轴上,△ABC是等腰三角形,写出所有满足条件的点C的坐标 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com